استخدمت عدة تقنيات لتطبيق المعادلة (35-8) ومشتقاتها في مشكلة تعيين الأطوار عمليا وسنقوم بشرح الطريقة التي استخدمها زكريازن Zachariasen سنة 1952 حيث نشرت في بحث مرفق بذلك الخاص بـ Sayre ومنذ ذلك التاريخ والمحاولات لم تكف عن محاولة استخدامها إلى أن شاع استخدامها وسميت بعد ذلك طريقة جمع الرموز symbolic addition method وقد قام كارل Karle وآخرون باستخدامها في تعيين التركيب بنجاح لعدد كبير من المركبات التي تحتوي على مركز تماثل.

الطريقة تعتمد على أن نبتدئ أولا بعدد محدود من الأطوار تستخدم بالاستعانة بالمعادلة (35-8) لتعيين أطوار أكثر وأكثر للحصول على عدد كاف لحساب الكثافة الإلكترونية باستخدام متسلسلة فوريير تمثل التركيب، والخطورة في هذه الطريقة تكمن في أن أي خطأ في تعيين أحد الأطوار في المراحل الأولى ينشأ عنه بناء هرم خاطئ من الأطوار، وللتغلب على ذلك نقوم ببناء أهرامات كثيرة من الأطوار ونختبرها لمعرفة الصحيح منها. وقد أصبح ذلك ممكنا مع تطور الحاسبات الإلكترونية في العصر الحالي.

أول مشكلة يجب التغلب عليها عمليا هي كيفية الحصول على أطوار يمكن استخدامها كبداية ومن حسن الحظ أنه يمكن اختيار عدد محدود غالبا ما يكون ثلاثة (وإن كان أحيانا أقل) ممكن أن تُعطى لها قيماً اعتباطا مع الأخذ في الاعتبار بعض القيود وهذه القيم الاعتباطية تكون هي القائمة الأولى.

ومشكلة تحديد الانعكاسات التي يمكن أن نعطي لها قيما للأطوار اعتباطا درست لكل المجموعات الفراغية وسنشرح بالتفصيل أبسط الحالات وهي الخاصة بالمجموعات الفراغية التي تحتوي على مركز تماثل في حالة النظام: ثلاثي الميل وأحادي الميل والمعيني القائم (triclinic; monoclinic; orthorhombic) وأي من هذه المجموعات الفراغية يمكن أن يكون شكل الوحدة البنائية لها كما هو موضح في شكل (3-8) الذي يحتوي على مراكز التماثل فقط دون عناصر التماثل الأخرى، في مثل هذه الأحوال يختار مركز الوحدة البنائية عند أحد مراكز التماثل.

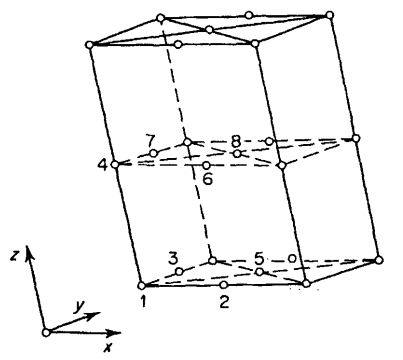
شكل (8-3)

وحدة بنائية في تركيب له مركز تماثل والمراكز المختلفة

وسنوضح فيما يلي أن تغير المركز للوحدة البنائية من مركز تماثل لآخر يؤثر فقط على الأطوار وليس القيمة العددية للمعادلات التركيبية للانعكاسات المحسوبة من مواقع الذرات، وعلى هذا فإنه لا مفاضلة بين أي من مراكز التماثل هذه.

حيث إن معادلة المعامل التركيبي لبلورة لها تماثل هي:

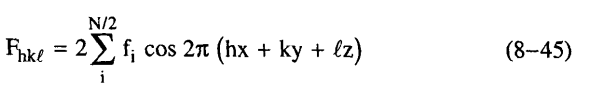
نفترض أن المركز سيتغير من الوضع (1) إلى الوضع (2) أي أنه سيصبح عند 1/2–x.

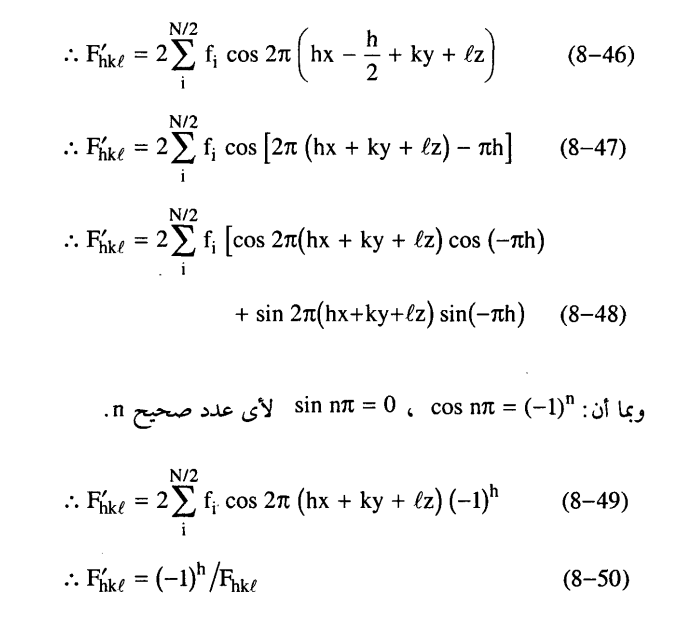
وعلى ذلك فان ازاحة المركز مسافة a/2 يؤدي الى تغيير إشارة كل الانعكاسات التي تكون قيمة h لها فردية ولكن لا تتغير قيمة |F|.

ويمكن بالمثل اشتقاق معادلات لكل إزاحة للمراكز المبنية في الشكل (8-3) توضح ان التغير بمقدار 1/2 على امتداد أي محور ينتج عنه تغير الإشارة للانعكاسات التابعة له التي تكون احداثيات ميلر لها كمية فردية أما الانعكاسات التي تكون احداثيات ميلر لها زوجية لا تتأثر.

وإذا كانت الإزاحة تتضمن اتجاهين من المحاور مثل a/2، b/2 للوصول للمركز رقم 5 مثلا فإن النتيجة تصبح:

ولا يحدث تغير في الإشارة الا اذا كان احد المعاملات h او k وليس كلامها لديه قيمة فردية.

الجدول (8-4) يوضح المجموعة الكاملة لتغيرات الإشارة لمجموعة من الانعكاسات كانت بداية الإشارة لها موجبة، وذلك لكل التجمعات الممكنة للإحداثيات الفردية والزوجية وكذلك المراكز، والجدول يعطينا القواعد التي تتبع في كيفية اختيار الإشارات، وحيث إن الإشارات للانعكاسات من النوع e e e لا تتغير أبدا فمن الواضح أنها إشارات ثابتة معتمدة على التركيب (structure invariants) ولا يمكن إعطاءها قيما حسب رغبتنا. أما باقي الفصائل فهي تكون موجبة لعدد أربعة مراكز للوحدة البنائية وتكون سالبة في حالة اختيار المراكز الأربعة الأخرى للوحدة البنائية.

وطالما أننا نجد إشارات موجبة وسالبة في الجدول لأي مجموعة من الانعكاسات فإن بعض الانعكاسات التي تتبع هذه المجموعة يمكن أن تعطي إشارة اعتباطيا حيث إن هذا يعني فقط اختيار مركز من الاثنين الممكنين.

جدول (8-4)

العلاقات بين الإشارات للمراكز الممكنة

وعلى سبيل المثال فإن الانعكاس من النوع o e e مثل 744 يعرف على أنه + (موجب) وهذا يقلل من العدد الممكن للمراكز الأربعة (1, 3, 4, 7) وإشارات الانعكاسات من النوع o e e أصبحت الآن ثابتة وعلى هذا لا نستطيع اختيار أي انعكاسات من هذه المجموعة، وباقي المجموعات كلها تعطى احتمالين بإشارة موجبة واثنين بإشارة سالبة وذلك للمراكز الأربعة التي تجعل المجموعة o e e موجبة. وعلى هذا أي انعكاس من هذه المجموعات على سبيل المثال 516 وهو من المجموعة o o e يمكن أن يأخذ الإشارة الموجبة وهذا يضيق عملية الاختيار للمراكز 1، 4 فقط وبعد ذلك أن يحدث اختيار لأحدهما وهذا الاختيار يجب الأخير يكون مقيداً أكثر مما قبله، فالمجموعة o e e ، o o e سبق أن ثبتت والاختيار من المجموعة e o e أيضا غير مسموح به، فكما يوضح الجدول (8-4) فإن الانعكاسات في المجموعة e o e تكون موجبة لكل من المركزين 1، 4 أي أن الإشارات لهذه المجموعة تكون قد حددت فعلا بالاختيارات التي أجريت ولا يمكن أن تختار اعتباطا. أما باقي المجموعات فكلها لها إشارة موجبة وإشارة سالبة لهذه المراكز وأي منها يمكن أن يستخدم لتحديد الإشارة الثالثة لتحديد المركز في النهاية.

ويمكن تلخيص المناقشة السابقة بدلالة الاتحادات المسموح بها إحداثيات ميلر باستخدام رياضيات التعادل Parity arithmetic التي تتضمن:

والقاعدة هي أنه بنفس الطريقة التي تجعل الانعكاسات التي تكون إحداثياتها كلها زوجية لا يمكن استخدامها، كذلك فإنه لا يُسمح باستخدام مجموعة من الانعكاسات اثنان أو ثلاثة يكون مجموع إحداثيات ميلر لها كلها زوجية e e e والجدول (8-5) يعطينا أمثلة للمجموعات المسموح وغير المسموح بها.

جدول (5-8)

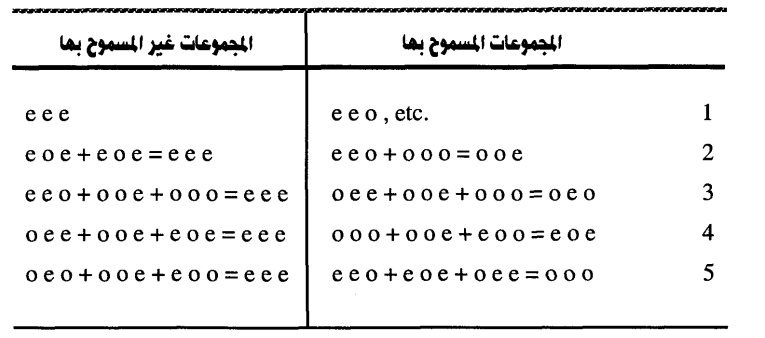
مما تقدم يتضح أنه مع الأخذ في الاعتبار القواعد السالفة الذكر فإنه يمكن إعطاء إشارات لعدد ثلاث انعكاسات، كما أنه من الممكن أيضا تعيين إشارات الانعكاسات التي ترتبط بعلاقات تماثل بالانعكاسات الثلاث الأصلية وعلى سبيل المثال فإنه في حالة النظام أحادي الميل يكون عندنا العلاقات الآتية إذا كانت l + h كمية زوجية تكون ...

وإلى جانب الإشارات التي تعطى لتحديد المركز فإنه يمكن أيضا إعطاء بعض الانعكاسات رموزا لتحديد إشارتها مثل a، b، c، .... حيث تضاف إلى الانعكاسات السالفة الذكر لتكون المجموعة الأساسية التي ستستخدم في إيجاد علاقة وتعيين إشارات جديدة، وفي النهاية نجد أنه في الإمكان تعيين الإشارات الصحيحة للرموز b ، a، ....

والدراسة الخاصة بعملية اختيار المركز وأطوار الانعكاسات التي لها علاقات بالانعكاسات الأخرى في حالة الشبيكات غير البسيطة والمجموعات الفراغية ذات التماثل العالي تكون مشابهة لذلك ولكنها أكثر تعقيدا والآن توجد برامج على الحاسب الآلي تعمل أوتوماتيكيا ليس فقط في حالة البلورات التي تحتوي على مركز تماثل ولكن أيضا في حالة البلورات التي ليس لها مركز تماثل، ولو أن تعيين الأطوار في مثل هذه الحالات يكون أكثر صعوبة حيث إن قيم الأطوار لا تكون محصورة بين 0° و º180 كما هو الحال في حالة البلورات التي لا تحتوي على مركز تماثل.

وفي حالة البلورات التي لا تحتوي على مركز تماثل فإنه إلى جانب الأطوار الثلاثة اللازمة لتحديد المركز يضاف طور رابع للاختيار بين الشكلين الإينتيومورفين enantiomorphic forms (هما الشكلان الذي يعطي أحدهما زاوية طور لأحد الانعكاسات قيمتها α ويعطي الشكل الثاني زاوية طور قيمتها α- لنفس الانعكاس) (شكل 8-4).

وفي هذه الحالة تعين الأطوار التي تتراوح قيمتها بين – π، + π

باستخدام العلاقات التي وضعها L. Karle & J. Karle . سنة 1966م وهي:

k_r تدل على الحدود p في مفكوك تيلر Taylor لدالة الجيب وهي تتطلب أن تكون البيانات المستخدمة هي فقط التي تكون قيمتها (E) كبيرة.

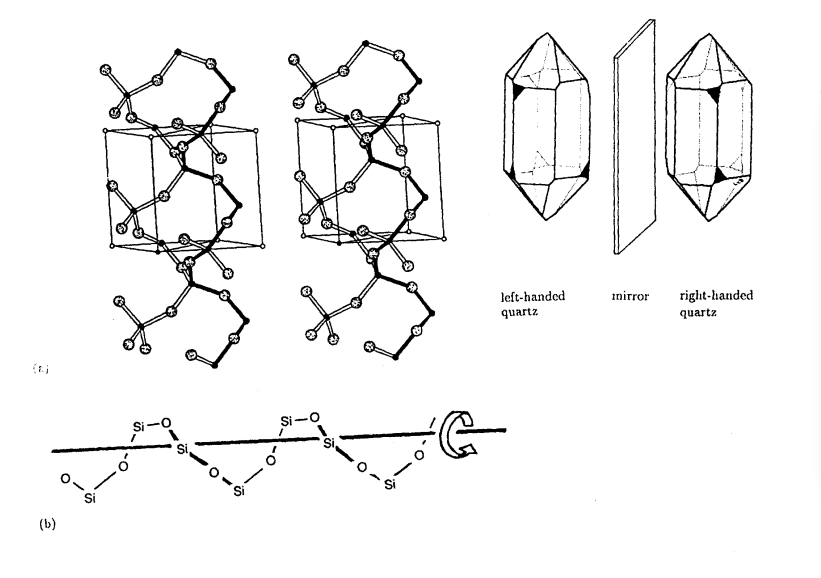
شكل (8-4) تركيب الكوارتز SiO₂

يوضح منظر مجسم له وشكل البلورة