القابلية البارامغناطيسية والديا مغناطيسية للبلورات
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المصدر:
علم البلورات والاشعة السينية
الجزء والصفحة:
ص66–69
2023-09-19
1880
من الخواص التي يمكن تمثيلها بكميات ممتدة من الرتبة الثانية خاصيتا القابلية المغناطيسية للمواد البارامغناطيسية والقابلية المغناطيسية للمواد الديامغناطيسية. ومن المقادير الفيزيائية المتعارف عليها:
H شدة المجال المغناطيسي.
I شدة التمغنط (المغنطة)، وهي العزم المغناطيسي لوحدة الحجوم من البلورة.
B الحث المغناطيسي أو كثافة التدفق.
وترتبط هذه المتجهات الثلاثة بعلاقة هي:
حيث 0μ مقدار ثابت يسمى نفاذية الفراغ وقيمته 107/4π في نظام MKS للوحدات.
وتتناسب شدة التمغنط طرديا مع شدة المجال في الكثير من المواد الأيزوتروبية، ما لم تكن شدة المجال كبيرة جدا.
حيث ꭓ هي القابلية المغناطيسية وهي بلا وحدات وإن أطلق عليها أحيانا القابلية المغناطيسية الحجمية إذا ارتبطت I بوحدة الحجوم وقد تكون ꭓ موجبة الإشارة كما في حالة المواد البارامغناطيسية أو سالبة في حالة المواد الديامغناطيسية. كما قد يطلق على القيم العددية للقابلية أسماء مختلفة مثل: القابلية النوعية، أو قابلية وحدة الكتل، أو القابلية الذرية أو الجزيئية (A ꭓ/ρ) - حيث ρ هي كثافة المادة، A الكتلة الذرية أو الجزيئية (الوزن الذرى أو الجزيئي). وإذا دمجنا المعادلتين (17-2) و(18-2) فإن:
والمقدار μ ما هو نفاذية المادة. كما يمكن تعريف المقدار:
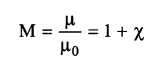
وهو ما يعرف بالنفاذية النسبية للمادة.
ولا تكون I موازية للمجال H بشكل عام في البلورات ولهذا تستبدل بالمعادلة (18-2) المعادلة الآتية:
حيث ijꭓ هي مركبات (عناصر) الكمية الممتدة للقابلية المغناطيسية.
وبغض النظر عما إذا كان I, H متوازيين أم لا، فإننا نستطيع كتابة المعادلة (17-3) كما يلي:
وهذه المعادلة هي التي تناظر المعادلة (20-2) ولكن في حالة البلورات ويمكن كتابتها بالتفصيل على النحو التالي:
وممتد النفاذية من الرتبة الثانية متماثل، أي أن:
ولذلك يمكن إسناد كل منهما إلى المحاور الرئيسية. وإذا طبق المجال H في اتجاه أي من المحاور الثلاثة المتعامدة فإن B تكون كلها متوازية مثلما هي الحال في المواد الأيزوتروبية. ومثال ذلك إذا كان H مطبقا باتجاه محور رئيسي Ox1 فإن:
وتتحدد قابلية البلورة تماما بمقادير واتجاهات القابليات الثلاث الرئيسية 1ꭓ، 2ꭓ، ꭓ3 وهي تخضع بطبيعة الحال لأية قيود يفرضها تماثل البلورة. (انظر الجدول 3-2).
الجدول (2-3)
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
اخر الاخبار
اخبار العتبة العباسية المقدسة
