تحويل المحاور Axes Transformation

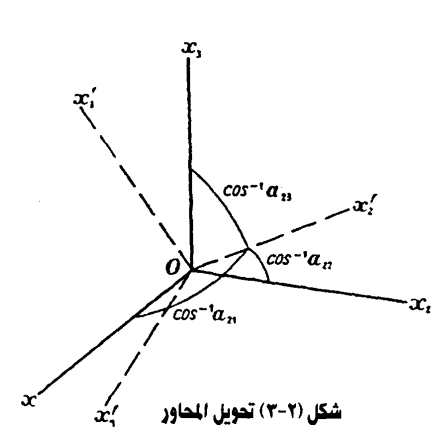
والمقصود من هذا المصطلح التحول من مجموعة من المحاور المتعامدة إلى مجموعة أخرى تشترك معها في نقطة الأصل وتكون وحدة القياس في اتجاه أي محور هي دائما نفس الوحدة. هب أننا أشرنا إلى المجموعة الأولى بالرموز x₁، x₂، x₃ وإلى الثانية بالرموزx'₁ ، x'₂، x'₃ الشكل (2-3) فإن العلاقة بين المجموعتين يمكن أن تكتب بدلالة جيوب تمام زوايا الاتجاهات.

الجدول (1-2)

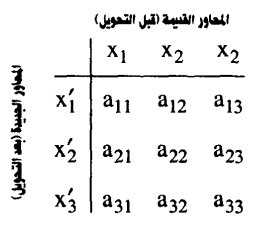
وعلى ذلك تكون جيوب تمام الاتجاهات الخاصة بالمحور x'₂ بالنسبة للمحاور x₃, x₂, x₁ هي: a₂₃, a₂₂, a₂₁ وجيوب تمام اتجاهات المحور x₃ بالنسبة للمحاور x'₁ ، x'₂، x'₃ هي : a₂₃, a₂₂, a₂₁. أي أن الترقيم السفلي الأول يشير إلى المحاور «الجديدة» والثاني إلى «القديمة».

ومن الواضح الآن أن a_ij هي جيب تمام الزاوية المحصورة بين المحاور x'_i، والمحاور x_j. وليست المقادير التسعة مستقلة عن بعضها البعض، وعلى العموم فإن

a_ij ≠ a_ji

• تحويل مركبات المتجهات

هب أن لدينا متجها ما 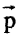 وأن مركباته في اتجاه المحاور x₃, x₂, x₁ هي p₃, p₂, p₁ (الشكل 2-4) وأن مركباته في اتجاه مجموعة أخرى من المحاور x'₁ ، x'₂، x'₃ هي: p'₁ ، p'₂، p'₃

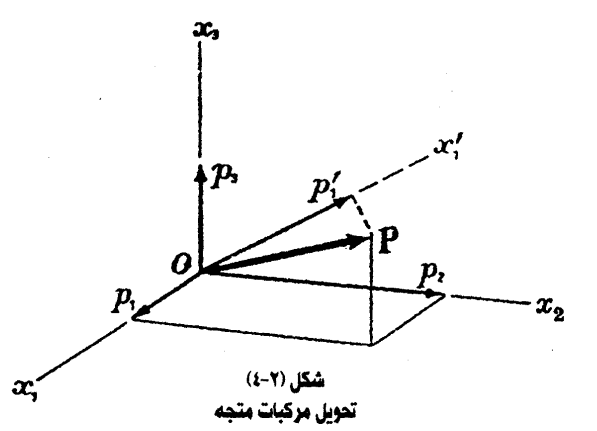
إن المركبة  p'₁تنتج عن تحليل p₁ ، p₂، p₃ في اتجاه x'₁ ، أي:

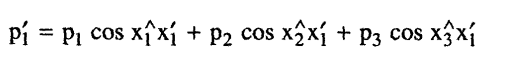
وعلى ذلك يكون:

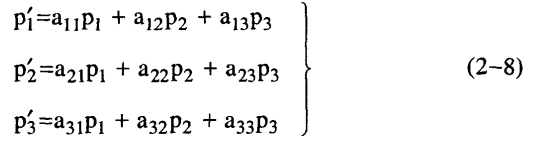
أو بشكل مختصر:

أما إذا سرنا بطريقة معكوسة؛ أي التعبير عن المركبات «القديمة» بدلالة «الجديدة» فإن:

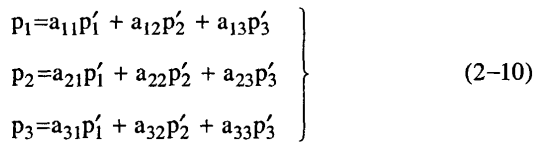
أو بشكل مختصر:

• تحويل إحداثيات نقطة ما

تعتبر إحداثيات النقطة (x₃, x₂, x₁) بالنسبة للمحاور Ox₃, Ox₂, Ox₁ هي مركبات المتجه OP في الشكل 2-4؛ ولذلك تكون الإحداثيات (x'₃, x'₂, x'₁) بالنسبة للمحاور Ox'₃, Ox'₂, Ox'₁ معطاة بالمعادلة:

• تحويل مركبات ممتد من الرتبة الثانية

إذا أردنا تحويل مركبات ممتد من الرتبة الثانية من مجموع محاور «قديمة» (x₃, x₂, x₁) إلى مجموعة محاور جديدة x'₃, x'₂, x'₁ وكانت T_ij تربط بين المتجهين  p وq فإننا نتبع الخطوات التالية باتجاه الأسهم:

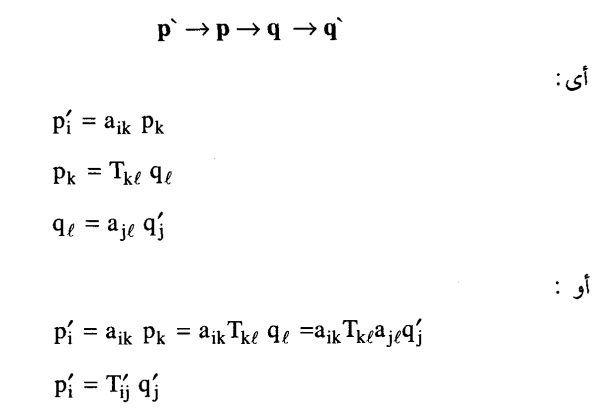
وبمقارنة المعادلتين الأخيرتين نجد أن:

وهذا هو قانون تحويل مركبات الكمية الممتدة (الممتد) من الرتبة الثانية. أما الصورة المعكوسة فهي:

• تحويل حاصل ضرب الإحداثيات

لقد وجدنا أن قانون تحويل ممتد من الرتبة الأولى (متجه) هو:

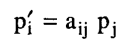
وهو في نفس الوقت قانون تحويل إحداثيات نقطة ما:

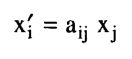
ومن ثم فإن قانون تحويل الممتد من الرتبة الثانية هو نفس قانون تحويل حاصل ضرب إحداثيين؛ أي أن مركبات كمية ممتدة T_ij تتحول مثلما يتحول حاصل الضرب x_ix_j. ويبين الجدول التالي (جدول2-2) قوانين تحويل مركبات كميات ممتدة من رتب مختلفة.

جدول (2-2)

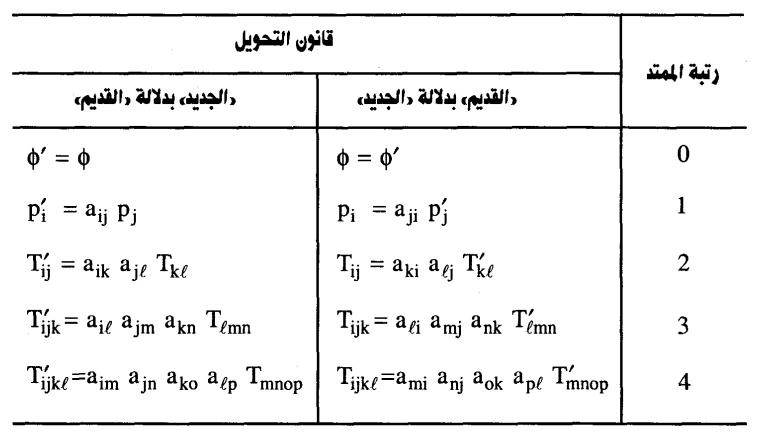
• التمثيل البياني للكميات الممتدة

يمكننا جعل الخاصية الفيزيائية شيئا ملموسا إذا قمنا بعمل التمثيل البياني للكمية الممتدة التي تصف تلك الخاصية. وسنبدأ بالنظر في المعادلة:

حيث S_ij هي نوع من المعاملات والمعادلة في صورتها المفصلة هي:

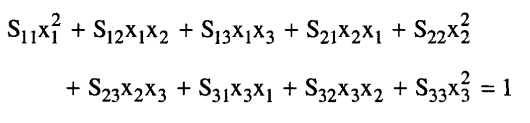
وإذا افترضنا أن S_ij = S_ji وجمعنا الحدود فإن:

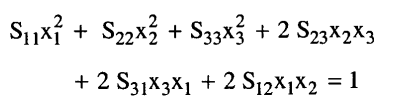
وهذه – في الواقع – معادلة سطح من الدرجة الثانية (تربيعي) ومسند إلى مركزه كنقطة أصل، وقد يكون هذا السطح بوجه عام هو سطح مجسم قطع ناقص أو سطح مجسم قطع زائد.

ويمكننا أن نستخدم قوانين تحويل المحاور الآتية:

حيث a_lj ، a_ki هي جيوب تمام الاتجاهات الخاصة بالمحاور بعد التحويل x' بالنسبة للمحاور قبل التحويل x.

وعلى هذا تتحول المعادلة (7-2) من مجموعة المحاور x_i إلى مجموعة جديدة x'_i:

حيث:

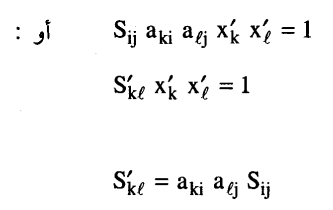
وهذا القانون شبيه بقانون تحويل الكمية الممتدة من الرتبة الثانية:

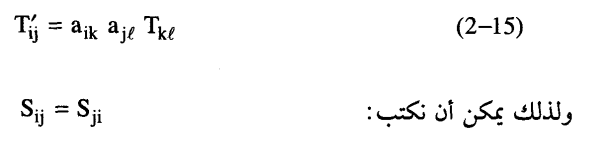
وعلى هذا يكون السطح الممثل بالمعادلة (14-2) خاصا بالمجسم التربيعي للكمية الممتدة S_ij. ومن الخواص المهمة لمثل هذا المجسم امتلاكه لمحاور رئيسية ثلاثة متعامدة فيما بينها. وإذا نسب المجسم إلى تلك المحاور فإن معادلته تصبح:

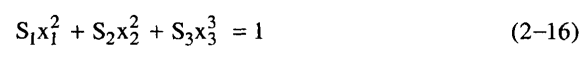
ومثلما يتخذ المجسم أبسط صورة عندما ينسب إلى محاوره الرئيسية فإن أي ممتد متماثل من الرتبة الثانية يمتلك نفس الخاصية.

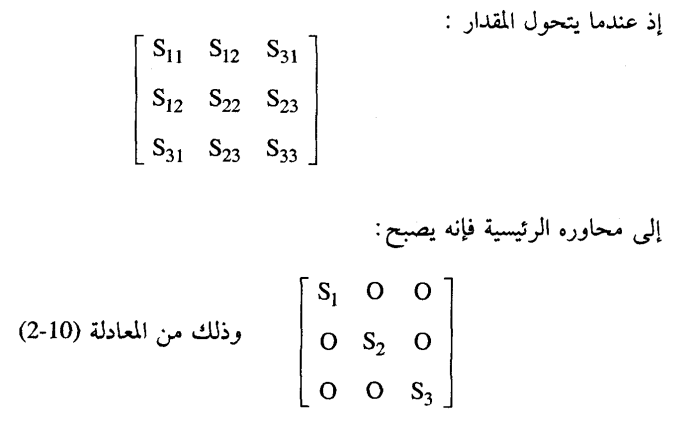
والكميات S₁، S₂، S₃ هي المركبات الرئيسية للمتد [S_IJ] أو للخاصية التي يمثلها.