تتحدد المستويات البلورية من حيث موقعها واتجاهها إذا علمت ثلاث نقط بشرط ألا تكون على خط مستقيم. وإذا وقعت كل نقطة على محور بلوري فإن المستوى قد يتحدد إذا علمت مواقع النقط على طول المحاور بدلالة الثوابت البلورية. فإذا كانت إحداثيات الذرات التي تحدد المستوى هي (4, 0, 0)، (0 ,1 ,0)، (2 ,0 ,0).

بالنسبة لمتجهات المحور بعيدا عن نقطة أصل معروفة فإن المستوى يتحدد بثلاثة أرقام هي 4، 1، 2.

على أنه قد يكون من الأجدى بالنسبة لتحليل التركيب البلوري أن نحدد اتجاه المستوى بدلالة ما يسمى إحداثيات ميلر التي يحددها الشكل (1-5) كما يلي:

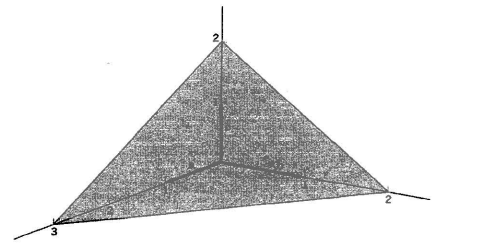
شكل (1-5)

يقطع هذا المستوى المحاور c, b, a عند a3، b2، 2c ومقلوبات هذه الأرقام هي 1/3، 1/2، 1/2 أما المعامل المشترك البسيط جعل النسبة بينها 2، 3، 3 وتكون إحداثيات ميلر (3 3 2)

1- يتم تحديد نقط تقاطع المستوى مع المحاور 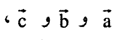   بدلالة الثوابت البلورية وقد تكون المحاور بدائية أو غير بدائية.

2- يتم بعد ذلك إيجاد مقلوبات هذه الأرقام ويحسب العـامل المشترك البسيط بينها لنحصل على ثلاثة أرقام تحمل فيما بينها نفس النسبة، ثم يعبر عن الناتج داخل قوسين هكذا: (h k l).

مثال: إذا كان مستوى ما يقطع المحاور في المسافات 4، 1، 2 فإن مقلوبات هذه الأرقام 1/4، 1، 1/2 وتكون إحداثيات «ميلر» هي (2، 4، 1)، أما إذا حدث التقاطع مع محور ما عند ما لا نهاية فإن الإحداثي المناظر يكون صفرا. ويوضح الشكل (1-6) إحداثيات «ميلر» لبعض المستويات الشائعة في بلورة مكعبية.

شكل (1-6)

إحداثيات «ميلر» لبعض المستويات المهمة في بلورة مكعبية ويلاحظ أن المستوى (200) يوازي المستوى (100)

وقد تعنى الإحداثيات ( (h k lمستوى واحدا أو مجموعة من المستويات المتوازية. وعندما يقطع المستوى محورا ما في الجانب السالب من نقطة الأصل فإن الإحداثي المناظر لذلك يكون سالبا وتوضع إشارة السالب فوقه هكذا: (h k l). وعلى هذا تكون إحداثيات أوجه المكعب الستة (وهي تمثل ستة مستويات) كما يلي:

(0 0 1)، (0 1 0)، (1 0 0)، (0 0 1̅)، (0 ̅1 0)، (̅1 0 0)، وتميز المستويات المتكافئة من حيث التماثل بأقواس ملتوية تحوى بداخلها إحداثيات «ميلر». أي أن مجموعة أوجه المكعب تصبح {0 0 1} وقد نذكرها ببساطة فنقول أوجه 0 0 1. أما إذا ذكر المستوى (0 0 2) فإننا نعني المستوى الموازي للمستوى (0 0 1)، ولكنه يقطع المحور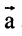 عند 1/2a

ويعبر عن إحداثيات اتجاه ما في البلورة بمجموعة من أصغر أرقام تمثل النسبة بين مركبات متجه له نفس الاتجاه المطلوب منسوبة إلى المحاور البلورية، وتكتب هذه الأرقام الصحيحة بين قوسين مربعين هكذا: [h k l] ومثال ذلك يصبح اتجاه المحور (x) في بلورة مكعبية مثلا هو [0 0 1]، أما المحور (y-) فيكون اتجاهه [0 ̅1 0]. ويلاحظ أن الاتجاه في البلورات المكعبية يكون دائما متعامدا مع المستوى الذي له نفس إحداثيات ميلر، وإن كان هذا الأمر ليس صحيحا على إطلاقه في النظم البلورية الأخرى.