عند التفكير في انحناء الفضاء الثنائي الأبعاد على غرار سطح الكرة - من الممكن أن نتخيله على شكل انحناء يقع في فضاء ثلاثي الأبعاد. لكن عندما يتعلق الأمر بالفضاء الثلاثي الأبعاد، لا يوجد بعد مكاني إضافي كي يستوعب عملية الانحناء. بدلا من هذا علينا الاعتماد على فحص الخصائص الهندسية للفضاء الثلاثي الأبعاد ذاته. ومع ذلك، فإن التمثيلات الثنائية الأبعاد للفضاء الثلاثي الأبعاد يمكنها أحيانًا أن تمنحنا فكرة عامة عما يحدث. يصح هذا تحديدا في حالة التناظر الكروي - شأن الانحناء الموجود في الفضاء المحيط الذي تسببه الشمس حيث أيُّ شريحة ثنائية الأبعاد عبر ذلك الفضاء (تمر عبر الشمس) تتساوى مع أي شريحة أخرى ثنائية الأبعاد هنا يصير البعد الثالث غير ذي أهمية؛ لأنه لا يحتوي على أي معلومات غير متاحة بالفعل من خلال البعدين الآخرين. في هذه الصورة التوضيحية، يمكننا تمثيل الفضاء الثلاثي الأبعاد بواسطة هذه الشريحة الثنائية الأبعاد، ثم استخدام البعد الثالث الخاص بهذه الصورة التوضيحية لاستيعاب عملية «الانحناء». في الشكل 2-14 نرى كيف أن الانحناء الكلي الناجم عن وجود الكرة الثقيلة (الشمس) يجعل الكرة الصغيرة (أحد الكواكب تدور حولها بدلًا من الانطلاق في خط مستقيم.

في الشكل 2-15 نرى بتفصيل أكثر نوعية الانحناء الذي تسببت فيه الشمس. لكن لِمَ يأخذ مثل ذلك الشكل؟ يعتمد ميل المنحنى في أي نقطة على المسافة بين هذه النقطة وبين مركز الشمس، وأيضًا على مقدار المادة الجاذبة الموجودة بين النقطة المختارة وبين مركز الشمس.

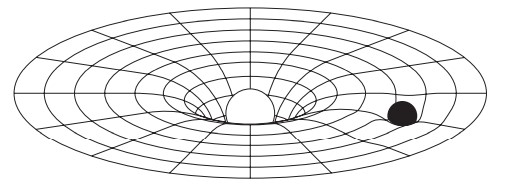
شكل 2-14: تمثيل للطريقة التي يتسبب بها انحناء الفضاء الناجم عن وجود الشمس في جعل الكوكب يدور حولها.

بينما نتدبر النقاط الأقرب والأقرب إلى الشمس، يظل مقدار المادة ثابتًا (كتلة الشمس)، لكن المسافة تقل؛ ومن ثَم يزداد ميل الانحناء. ويستمر هذا حتى نصل إلى حافة الشمس عند النقطةR . وبالتحرك في النطاق الداخلي للشمس الآن، تستمر المسافة إلى المركز في التناقص، لكن الآن يقل مقدار الكتلة الموجودة بين النقطة المختارة والمركز؛ وهو التأثير الذي يميل إلى التقليل من الانحناء في الواقع، يؤدي مجموع هذين التأثيرين إلى خفض إجمالي في الانحناء؛ بحيث إنه عند الوصول إلى مركز الشمس، يكون الانحناء قد استوى. وهذا هو المتوقع؛ نظرًا لأن الشمس لا تمارس أي قوة جذب عند نقطتها المركزية. وما ينطبق على الشمس ينطبق بالمثل على النجوم الأخرى، وعلى الكواكب؛ وبذا فهي تنتج انحناء أشبه بالانحناء المبين في الشكل 2 -15.

لكن مجددًا دعوني أؤكد على أنه رغم كون هذه المخططات مفيدة في تصور ما يحدث في الواقع، فإننا من الناحية العملية لا نرى الفضاء الثلاثي الأبعاد وهو ينحني داخل بعد مكاني آخر من نوع ما بدلا من ذلك علينا الاعتماد على الخصائص الجوهرية للفضاء نفسه. ما الذي يعنيه هذا إذن؟ سنتناول مثالا محددًا عن جسم متناظر كرويا كالشمس ونتساءل: كيف له أن يؤثر على الزمكان من حوله؟

نعرف بالفعل القليل عن الكيفية التي يتأثر بها الزمن. فمن منظور الراصد البعيد عن الشمس، تبدو الساعة الأقرب إلى الشمس وكأنها تسير ببطء؛ وذلك لأنها واقعة تحت تأثير الانزياح الأحمر الجذبوي. لكن بأي مقدار؟ كان كارل شفارتز تشيلد أول من يحل معادلات أينشتاين الخاصة بحالة الجسم المتناظر كرويًّا.

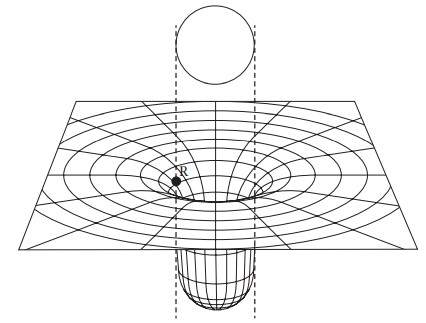
شكل 2-15: منظر جانبي لانحناء الفضاء الذي تسببه الشمس يبين كيف أن الانحناء يقل داخل الشمس.

يتطلب الحل قدرًا كبيرًا من الحسابات الرياضية، لكن النتيجة النهائية بسيطة إلى حدٍّ ما؛ إذ إنه من منظور الراصد البعيد، يبدو معدل حركة الساعة وقد تباطأ بمعامل قدره  ^1/2(1 — 2mG/rc²)؛ حيث m كتلة الشمس، وG ثابت الجاذبية، وr المسافة التي تبعدها الساعة عن مركز الشمس، وهي سرعة الضوء المعتادة. ونذكر هنا أنه إذا كانت قيمة r كبيرة، تقترب قيمة التعبير الرياضي من الرقم 1 بمعنى أنه حين تكون الساعة بعيدة عن الشمس، تبدو وكأنها تسير بالمعدل الطبيعي. وكلما اقتربت الساعة من الشمس، تباطأت حركتها. وبالنسبة للنجوم الأثقل من الشمس - أي التي تكون كتلتها كبيرة - يكون التأثير أكبر، وهذا أمر متوقع. هذا بخصوص الزمن، فماذا عن المكان؟ يبين حل شفارتز تشيلد أن المكان يتأثر في على سبيل المثال الاتجاه الشعاعي. تخيل أن عددًا من المساطر موضوع واحدة تلو الأخرى على امتداد المسافة الفاصلة بين الراصد والشمس من منظور الراصد، تبدو المساطر وكأنها تقصر؛ فكلما اقتربت المسطرة من الشمس، قصر طولها. والمعامل الذي تقصر به المساطر نحصل عليه من التعبير الرياضي عينه الذي استخدمناه في حالة الإبطاء الزمني، وهو:
^1/2(1 — 2mG/rc²). ومرة أخرى نرى أنه إذا كانت قيمة r كبيرة، تقترب قيمة التعبير الرياضي من الرقم 1 وتبدو المسطرة وكأن طولها طبيعي. لكن إذا كانت قيمة r صغيرة، أو قيمة m كبيرة، يزداد انكماش المسطرة.

ما علاقة هذا بسرعة الضوء؟ تخيل أن نبضة من الضوء تنطلق من الساعة مبتعدة عن مجال الجاذبية ومتجهة نحو الراصد. تبدأ النبضة في منطقة يكون الزمن فيها قد تباطاً. يعني هذا أن كل شيء يحدث هناك تباطأت سرعته من منظور الراصد البعيد. وهذا يسري على سرعة الضوء؛ فتأخذ وقتًا أطول كي تقطع مسافة كل مسطرة من المساطر الموضوعة على امتداد المسافة إلى الراصد. لكن ليس الزمن وحده هو ما يتباطأ في منطقة الساعة، بل ينضغط المكان أيضًا في الاتجاه الشعاعي الذي تتحرك النبضة فيه. يعني هذا أنه من منظور الراصد البعيد يقطع الضوء مسافة تقل عن المتر في كل مرة يجتاز فيها مسطرة طولها متر. وهذا عامل ثان يؤدي إلى إبطاء نبضة الضوء. وبذا يكون على الضوء أن «يجر» نفسه مبتعدا عن الشمس.

هل تتباطأ سرعة الضوء؟ أليس في هذا خرق لإحدى المسلمتين اللتين تقوم عليهما النظرية النسبية؟ كلا. تحدثت تلك المسلمة تحديدًا عن أطر القصور المرجعية، ونحن هنا لا نتعامل مع إطار قصوري. ففي الزمكان المنحني الذي تنتجه الجاذبية، لا يوجد ما يمنع سرعة الضوء من أن تتخذ قيمًا مختلفة عن قيمتها المعتادة.

إلى الآن، حصرنا اهتمامنا على الصورة التي سيبدو عليها الموقف من منظور الراصد البعيد. فماذا عن راصد في حالة سقوط حر قريب من الساعة محل النقاش؟ هذا الراصد يكون في إطار مرجعي قصوري محلي، وتبدو بيئته المباشرة طبيعية إلى حد بعيد؛ فساعته تسير بمعدلها الطبيعي، والمساطر المترية جميعها لها الطول نفسه، وسرعة الضوء في منطقته هي السرعة المعتادة. من المهم هنا أن ندرك أنه مثلما كانت أي منطقة صغيرة على سطح الكرة أو السرج تكاد تكون مستوية - وأنه كلما صغرت المنطقة صارت أقرب إلى الاستواء - فإنه في الزمكان الرباعي الأبعاد أيضًا، إذا تدبرنا موقف راصد في حالة سقوط حر في منطقة محلية صغيرة من ذلك الزمكان، فسيبدو لنا وقتها أن الزمكان «مستو»؛ بمعنى أنه يخضع لقواعد النسبية الخاصة؛ وبذا يمكن التفكير في الزمكان المنحني حول الشمس مثلًا وكأنه حاشية مرقعة من المناطق المحلية الصغيرة يمكن التعامل مع كل واحدة منها من خلال قواعد النسبية الخاصة. وحده الراصد البعيد هو من يستطيع استيعاب الصورة الكلية الشاملة لما يحدث في الزمكان القريب من الشمس والبعيد عنها، وهو الوحيد القادر على إدراك سماته المنحنية.

عند تحديد المقدار الذي يبدو الزمن وقد تباطاً به ―وتبدو المسافة وقد انكمشت به — من منظور الراصد البعيد تحدثنا عن المعامل ^1/2(1 — 2mG/rc²). ربما خطر لك أن تتساءل عما سيحدث لو أن قيمة r كانت صغيرة للغاية إلى درجة يساوي معها الحد الثاني للمعادلة 1 ويقل الناتج الكلي إلى صفر. ألن يعني هذا أن الزمن سيتوقف وأن المساطر المترية سيصير طولها صفرًا؟ علينا توخي الحذر هنا؛ فحل شفارتزتشيلد (وبالتبعية مدى ملاءمة ذلك المعامل) ينطبق فقط في الخارج؛ حيث تكون كتلة الشمس مركزة. بعبارة أخرى فيما وراء النقطة R في الشكل 2-15 بالنسبة للشمس، فإن قيمة التي من شأنها أن تجعل المعامل يساوي صفرًا ستكون قيمتها داخل الشمس واحدًا صحيحًا؛ لأن نسبة بسيطة للغاية من الكتلة هي التي ستظل موجودة داخل نصف قطر الكرة.. إذن، بالنسبة للشمس، من المستحيل أن يقل المعامل حتى يصل إلى صفر. إلا أن هذا ليس الحال دومًا؛ فهناك أجرام في الكون مضغوطة للغاية إلى درجة يمكن معها الوفاء بهذا الشرط. وهذا يأخذنا إلى موضوع الثقوب السوداء الساحر. إذن، ما هي الثقوب السوداء؟ وكيف تتكون؟

رأينا كيف أن النجوم تستمد طاقتها من عمليات الاندماج النووي. ومن البديهي أن -شأنها شأن أي جسم مشتعل - سيأتي عليها يوم ينفد فيه الوقود منها. ويعتمد ما سيحدث عندئذ إلى حدٍّ بعيد على مدى ثقل النجم ومن ثَم مقدار شدة جاذبيته. بالنسبة للنجوم متوسطة الحجم كشمسنا، بعد الاحتراق بثبات لمدة 10 آلاف مليون عام، سينتفخ النجم ويصير عملاقا أحمر. ثم سيطرح طبقاته الخارجية، بينما ينهار القلب على نفسه مكونا «قزمًا أبيض» ساطعًا. ثم سيخبو هذا القلب ويصير جمرة باردة.

أما النجم الذي تزيد كتلته عن كتلة الشمس بثمانية أضعاف فستنتهي حياته النشطة بالانفجار كمستعر أعظم (سوبرنوفا). سينهار قلبه تحت وطأة الجاذبية لدرجة أن الإلكترونات - التي توجد في المعتاد خارج نواة الذرة - ستدفع إلى داخل النواة نفسها، حيث تنضم إلى البروتونات والنيوترونات. بعد ذلك ستتحد مع البروتونات لتكون المزيد من النيوترونات، إضافةً إلى النيوترينوات (والنيوترينوات المنبعثة هي المسؤولة عن دفع المادة إلى الخارج أثناء الانفجار). وهكذا يتبقى لدينا قلب من النيوترونات يُعرف باسم (النجم النيوتروني) إن النجم النيوتروني تساوي كتلته في المعتاد 1.4 كتلة الشمس، ومع ذلك لا يتجاوز نصف قطره عشرة كيلومترات. وتبلغ شدة الجاذبية على سطح النجم النيوتروني 10¹¹ × 2 مرات قدر الجاذبية على الأرض.

لو أن كتلة النجم كانت تبلغ في البداية 20 مرة ضعف كتلة الشمس، فسينتج عن انفجار المستعر الأعظم نجم نيوتروني تتجاوز كتلته ضعفي كتلة الشمس، إلا أنه بالنسبة لهذه الكتلة، تكون الجاذبية شديدة للغاية لدرجة أنه لا شيء يستطيع مقاومتها، وسيستمر النجم النيوتروني المتكون في الانهيار على ذاته إلى أن تتركز مادته كلها في نقطة وحيدة؛ منطقة متناهية الصغر حجمها صفر وكثافتها لانهائية. وهكذا يولد الثقب الأسود، كما أسماه جون ويلر في ستينيات القرن العشرين إلا أن هذه الظاهرة جرى التنبؤ بها قبل ذلك بكثير، في عام 1939 تحديدًا، على يد روبرت جيه أوبنهايمر وهارتلاند سنايدر استنادًا إلى نظرية أينشتاين.

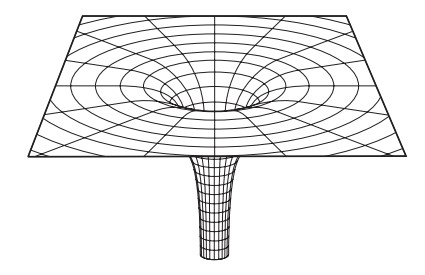
شكل 2 - 16: منظر جانبي لانحناء الفضاء الذي يسببه ثقب أسود.

يوضح الشكل رقم 2 - 16انحناء الفضاء الذي يسببه الثقب الأسود. يُعتقد أن الانحناء يستمر وصولاً إلى نقطة تفرد تتجمع فيها المادة كلها. أما عن قوة الجاذبية فستدنو هذه القوة من اللانهائية كلما اقتربنا من المركز وأي شيء يسقط في الثقب الأسود سيسحق إلى نقطة وحيدة في المركز على الأقل، هذه هي النتيجة التي تنبئنا بها معرفتنا الفيزيائية الحالية. لكن مصدر القلق هو أن معرفتنا الفيزيائية الحالية لا يمكنها التعامل مع نقاط التفرد. فنحن نعرف أننا عندما نتعامل مع الأجسام الصغيرة للغاية على المستوى دون الذري، فإن كل شيء يخضع لقواعد نظرية الكم، ونحن لا نعرف بعد كيف نجمع بين فيزياء الكم والنظرية النسبية. إذن، ربما تخبئ لنا الطبيعة مفاجأة ما. ومع هذا، ليس لدينا بديل في الوقت الحالي سوى تقبل النتيجة القائلة بأن كل شيء سيسحق إلى نقطة وحيدة.

في هذه الحالة - وعلى العكس من الشمس - سيكون لهذا الجرم مسافة تبتعد عن مركزه يقل فيها التعبير ^1/2(1 — 2mG/rc²) وصولاً إلى الصفر. وسيكون هذا عند نصف القطر k الذي نحصل عليه من المعادلة التالية:

k = 2mG/c²

ويطلق على k اسم «نصف قطر شفارتز تشيلد». ويحد نصف قطر شفارتز تشيلد سطحًا كرويا يسمى أفق الحدث، مركزه نقطة تركز الكتلة. يمكن توضيح المغزى من هذه المسافة بالطريقة التالية: تخيل أن ثمة مركبة فضائية تهوي نحو ثقب أسود، وبينما تدنو المركبة من أفق الحدث فهي تبدو للراصد البعيد وكأنها تبطئ من سرعتها. هذا هو التأثير المزدوج لإبطاء الزمن وتقلص الأطوال الشعاعية كلما اقتربنا من المركز. عند أفق الحدث ذاته، تبدو المركبة وكأنها توقفت، بل وكأنها عالقة هناك لأجل غير مسمى؛ سبب هذا هو أن الضوء الصادر عن المركبة يجب عليه أن يجر نفسه ببطء بعيدًا عن تلك المنطقة. وعند أفق الحدث ذاته، يستغرق الضوء وقتًا لانهائيا كي يصل إلى الراصد؛ ومن ثم يبدو الجسم وكأنه ساكن بلا حراك. لكن من الناحية العملية لن تبدو المركبة كذلك لوقت طويل. فرغم أن المركبة تبدو من منظور الراصد البعيد وكأنها توقفت عند أفق الحدث، فإن المركبة ذاتها مرقت من هذه المنطقة بسرعة كبيرة إلى حدٍّ ما متجهة صوب الثقب الأسود. لقد بعثت كمية محدودة فقط من الضوء خلال توقفها الوجيز في تلك المنطقة؛ لذا، بمجرد أن يزحف ذلك الضوء وصولا إلى الراصد، لا يتبقى منه أي شيء، وسريعا ما تتلاشى شدة الضوء وتخبو الصورة تمامًا.

يجب هنا التأكيد على أن هذا ما ستبدو عليه الأمور من منظور الراصد البعيد. فكيف ستبدو الأمور من منظور رائد الفضاء الموجود داخل المركبة؟ من منظور رائد الفضاء، بينما تهوي المركبة نحو الثقب الأسود، يكون رائد الفضاء في البداية داخل إطار قصوري 

وتبدو البيئة المحيطة طبيعية. لا شيء غريب بخصوص الزمن أو المسافة أو سرعة الضوء. وسيمر رائد الفضاء عبر أفق الحدث وهو غير واعٍ إلى أنه من اللحظة الحالية صار مصيره محتومًا. لكن لا يوجد ما ينبئ رائد الفضاء بأنه يجتاز نقطة اللاعودة، وأنه من اللحظة الحالية لا مهرب له. بعد الدخول في أفق الحدث، يستمر كل شيء في الاندفاع بلا هوادة صوب مركز الثقب الأسود. وهذا ينطبق على الضوء مثلما ينطبق على أي شيء آخر. فالثقوب السوداء لا ينبعث منها أي ضوء؛ ولهذا سميت بهذا الاسم.

ينتهي الحال برائد الفضاء ومركبته وقد انسحقا في نقطة وحيدة في مركز الثقب. ومن المهم أن ندرك أن هذا النوع من الانسحاق لا يشبه البتة ظاهرة تقلص الأطوال التي تعرضنا لها في سياق النسبية الخاصة. فكما تذكر - في حالة تقلص الأطوال – فإن رائد الفضاء ومركبته لم يستشعرا أي شيء؛ لأن ذرات جسديهما تقلصت هي الأخرى؛ ومن ثم لم تعد بحاجة لنفس المكان الذي توجد فيه. لكن السقوط في ثقب أسود سيكون أمرًا مختلفًا تمامًا؛ فعندما يسقط رائد الفضاء وقدماه جهة الثقب الأسود، سيشعر أن جسده يستطيل، كما لو كان موضوعًا على آلة التعذيب المسماة بالمخلعة. سبب هذا هو أن قدميه أقرب إلى مركز الثقب؛ ومن ثَم فهما يتأثران بمجال جاذبية أقوى من ذلك الذي يؤثر على رأسه، الأبعد قليلًا عن مركز الثقب. وبينما تتواصل عملية الاستطالة، يزداد جانباه انسحاقا. وفي النهاية، ينتهي الحال به وقد انسحق في نقطة وحيدة، وقد مات بكل تأكيد! بالنسبة للنجم الذي انتهى به الحال كثقب أسود وتبلغ كتلته مثلًا عشرة أضعاف كتلة الشمس، تُبين المعادلة  k = 2mG/c²أن قيمة k ستبلغ نحو 10 كيلومترات. على هذه المسافة من المركز، تكون القوى المدية المؤثرة على جسد رائد الفضاء الساقط عند أفق الحدث مهولة بالفعل. سيكون الأمر أشبه بوضع رائد الفضاء على مخلعة مع تعليق ثقل قدره مليار كيلوجرام في قدميه. هذا هو الوضع في حالة «الثقب الأسود النجمي»؛ أي الثقب المتكون نتيجة انهيار أحد النجوم. حيث أن هذه ليست الطريقة الوحيدة لتكون الثقوب السوداء؛ إذ يُعتقد الآن أن أغلب المجرات تؤوي ثقوباً سوداء في قلوبها؛ والمعروفة باسم «الثقوب السوداء المجرية». تتكون هذه الثقوب من خلال تقارب النجوم القريبة من مركز المجرة بعضها من بعض، ثم اصطدامها واندماجها؛ ومن ثَم انهيارها مكونة ثقبًا أسود ضخمًا. في عام 1974 اكتشف أن مجرتنا - مجرة درب التبانة - تُؤوي ثقبًا أسود في مركزها تبلغ كتلته 3 ملايين مرة قدر كتلة الشمس. ويبدو أن أغلب المجرات الأخرى تحوي أجرامًا سوداء فائقة الصخامة يُعتقد أنها ثقوب سوداء. وقد ابتلع بعضها بالفعل مليارات النجوم.

من خلال المعادلة k = 2mG/c²، نرى أن نصف قطر أفق الحدث يتزايد طرديا تزايد الكتلة. ومن المعروف أن القوة المديَّة الموجودة في أفق الحدث تتناسب عكسيا مع مربع الكتلة. وعليه فإنه حتى في حالة الثقب الأسود المجري الصغير الذي يحوي مليون كتلة شمسية ستقل القوة المدية عند نصف قطر شفارتزتشيلد بمعامل قدره 10¹²، وهو ما يعني أن رائد الفضاء سيمر من أفق الحدث دون تأثير يذكر (لكن بالطبع ما هذه إلا مهلة مؤقتة؛ إذ ستعمل القوى المدية القوية عملها على المسافات الأقل من هذا).

قلنا إن الثقوب السوداء النجمية تتكون عندما تنهار النجوم فائقة الضخامة. لكنَّ ثمة شيئًا واحدًا لم نذكره بعد وهو حقيقة أن أغلب النجوم - شأن الكواكب - لها زخم زاوي؛ أي إنها تدور حول محورها. يجب أن يظل الزخم الزاويُّ محفوظا؛ لذا رغم فقدان بعض من الزخم الزاوي بسبب المادة التي لفظها النجم خلال انفجاره كمستعر أعظم إبان انهياره، فإن الثقب الأسود ذاته من المتوقع أن يحافظ على غالبية الزخم الزاوي الأصلي للنجم. وهذا يجعل الأمور أكثر تعقيدًا. فحل شفارتزتشيلد لمعادلات أينشتاين لم يعد صالحًا. وتعين علينا الانتظار حتى عام 1963 ليخرج روي كير بحل للثقوب السوداء الدوارة. وقد جلب لنا حل كير نتيجة مثيرة للاهتمام للغاية وهي أن الثقب الأسود الدوار يجر الزمكان القريب منه حوله كالدوامة الملتفة والجسم الساقط على نحو مباشر صوب الثقب الأسود سيجد نفسه وقد انجرف تدريجيًّا داخل هذه الحركة الدوارة. بالنسبة للثقب الأسود الدوار، يمر الجسم الساقط أولا عبر سطح يعرف باسم «الحد الساكن». وهذا الحد يعد بداية المنطقة المسماة (مجال أرجو) التي تمتد وصولا إلى أفق الحدث. في مجال أرجو، يكون مد الزمكان الدوار قويًّا للغاية لدرجة أنه لا شيء - ولا حتى مركبة فضائية تخيلية ذات قوة دافعة لانهائية - يمكنه البقاء ساكنا، بل سيكون عليه الدوران حول مركز الثقب. فقط خارج الحد الساكن من الممكن للمركبة الفضائية التي تشغل محركاتها أن تظل ساكنة.

حاليا، تعكف مهمة فضائية تدعى «مسبار الجاذبية ب» على اختبار عملية تباطؤ الإطار المرجعي. وتتكون هذه المهمة من أربعة جيروسكوبات فائقة الدقة. في الفضاء الحر ستحافظ هذه الجيروسكوبات على اتجاه محاور دورانها إلى ما لا نهاية. إلا أن المسبار يدور حول كوكب الأرض، وانحناء شفارتزتشيلد للفضاء الذي تسببه جاذبية الأرض من المفترض أن يسبب انحرافًا في قراءة الجيروسكوبات قدره 0.0018 درجة كل عام. علاوةً على ذلك، من المفترض وجود تأثير إضافي طفيف ناتج عن تباطؤ الإطار المرجعي قدره لا  يتجاوز 0.000011 درجة كل عام. هذا أشبه بالنظر إلى شعرة من على مسافة ربع ميل. وحتى كتابة هذه السطور لا نزال في انتظار النتائج.

تفقد الأجسام هويتها حين تسقط في ثقب أسود. على سبيل المثال، عندما تنسحق الأجسام في نقطة وحيدة، لا يكون لها أي حجم أو شكل مميز. لا يعني هذا أنها تفنى من الوجود تمامًا؛ فأي كتلة كان الجسم يملكها تُضاف إلى كتلة الثقب الأسود. ما الذي يتبقى أيضًا؟ من السمات المحفوظة كتلة الثقب الأسود، وسمة أخرى هي الزخم الزاوي. أيضًا الشحنة الكهربية تظل محفوظة؛ لذا، أيا كانت الشحنة التي كان يحملها الجسم الساقط فهي تظل محفوظة وتضاف إلى الشحنة الإجمالية للثقب الأسود. وهذا كل ما في الأمر؛ فقط الكتلة والزخم الزاوي والشحنة الكهربية. أما بقية السمات الأخرى للأجسام التي سقطت في الثقب، ومن ثَم صارت جزءًا منه، فتصير نسيا منسيا.

قد تفكر قائلًا: كل هذا يبدو معقولاً بدرجة كبيرة، لكن هل من دليل على وجود الثقوب السوداء؟ فعلى أي حال ثمة مشكلة جلية تتعلق بالعثور على الثقوب السوداء، وهي أنها سوداء معتمة؛ أي لا تبعث أي ضوء، علاوةً على أنها تبتلع أي ضوء كان من الممكن أن ينعكس عنها. فهذه الثقوب خفية بكل ما تحمله الكلمة من معنى.

هل تذكر فيلم الرجل الخفي؟ لم يكن بمقدور أحدهم رؤيته بصورة مباشرة، لكن كان بإمكانهم رؤية التأثيرات التي يحدثها على بيئته المحيطة. وهذا تحديدا هو النهج الذي نتبناه عند البحث عن الثقوب السوداء. فنحن نبحث عن نجم يمر بتغيرات دورية في ترددات الضوء المنبعث عنه، وسيكون سبب ذلك هو إزاحة دوبلر التي تحدث مع ابتعاد النجم عنا ثم اقترابه منا. هذه الحركة من السمات المميزة للنظم النجمية الثنائية التي تتكون من نجمين يدوران حول مركز كتلتهما المشترك. وفي المعتاد يكون من الممكن رؤية أحد هذين النجمين. لكن في بعض الأحيان يبدو أن ثمة نجمًا واحدًا وحسب، أما رفيقه فلا يُرى من واقع حركة النجم المرئي يمكننا حساب كتلة رفيقه. وإذا تجاوزت الكتلة 3 أضعاف كتلة الشمس، فمن المحتمل أن يكون هذا الرفيق ثقبًا أسود. تتعزز هذه الاحتمالية إذا كان النجم المرئي عملاقا أحمر؛ أي نجمًا منتفخًا بشدة. وفي بعض الأحيان نتمكن من رؤية الطبقات الخارجية للنجم المرئي وهي تُجذب ناحية الرفيق الخفي مطلقة الأشعة السينية بينما يجري امتصاصها بسرعة في جوف الثقب الأسود.

في عام 1972 اكتشف توم بولتون أن النجم المسمى «الدجاجة إكس-١» يظهر هذا السلوك تحديدًا. قدرت كتلة الشريك الخفي بسبعة أمثال كتلة الشمس. وكان هذا النجم مصدرًا لأشعة سينية متذبذبة بسرعة كبيرة. كان التذبذب في المعتاد يحدث كل جزء على المائة من الثانية. أشارت هذه الفترة إلى أن مصدر الأشعة السينية - أيا كان - لا يمكن أن يكون كبيرًا للغاية. يقطع الضوء نحو 3 آلاف كيلومتر أي حوالي ربع قطر الأرض) في هذه الفترة الزمنية، ومن ثَم يبدو أن هذا يضع حدا أقصى لحجم الجرم الذي يطلق هذه الأشعة السينية. بعبارة أخرى المنطقة صغيرة؛ على نحو يؤكد أن الانبعاث صادر من النطاق اللصيق لثقب أسود. ووقت كتابة هذه السطور، ثمة نحو 20 مثالاً معروفًا على الأنظمة الثنائية، التي يعد أفضل تفسير لها هو أن أحد النجمين المكونين لها هو في الواقع ثقب أسود نجمي؛ وبعض الأمثلة أقوى حتى من نجم الدجاجة إكس-1.

ماذا عن أدلة وجود ثقوب سوداء عملاقة في مراكز المجرات؟ تدور نجوم أي مجرة حول مركزها. في البداية قد يفترض المرء أن ما يبقى على النجوم في مسارها هو قوة الجاذبية الخاصة بكل النجوم الأخرى الأقرب إلى مركز المجرة من النجم المتحرك في مداره. لكن اكتُشف أن النجوم القريبة من مركز المجرة تدور على نحو أسرع بكثير مما هو متوقع وفق هذا المبدأ. وعليه، يخلص المرء إلى أنه من أجل توفير قوى الجذب الكافية للحفاظ على النجوم في مداراتها، يجب أن تفوق الكتلة الجاذبة القريبة من مركز المجرة كتلة جميع النجوم المرئية بكثير. وهذا يقودنا إلى استنتاج أنه في مركز المجرة ذاته لا بد من وجود ثقب أسود فائق الضخامة ابتلع بالفعل العديد من النجوم؛ ومن ثم جعلها جميعًا غير مرئية.

دليل آخر يشير إلى وجود الثقوب السوداء فائقة الضخامة يأتينا من «المجرات النشطة». هذه المجرات تبدو مثل المجرات العادية فيما عدا أنها تطلق انبعاثات من قلب صغير منطمر داخلها. إن نواتج هذه الانبعاثات. أشعة تحت حمراء وموجات راديوية وأشعة فوق بنفسجية وأشعة سينية وأشعة جاما قد تكون متباينة بشدة وساطعة للغاية مقارنة ببقية المجرة. يمكن تفسير هذا بالقول إن المادة يجري تكثيفها بواسطة منطقة صغيرة مركزية - ثقب أسود - مع انبعاث كميات كبيرة من طاقة الجاذبية. ثمة تأكيد آخر على وجود الثقوب السوداء يأتينا من «النجوم الزائفة». هذه عبارة عن أجرام ساطعة بدرجة استثنائية تقع على مسافات بعيدة للغاية عنا. وكلما نظرنا أبعد في جوف الكون وجدنا المزيد من النجوم الزائفة. وكما هو معروف، كلما نظرنا إلى جرم سماوي أبعد، يعني هذا أننا نعود أكثر إلى الماضي (بسبب الزمن المحدد الذي يستغرقه الضوء في الوصول إلينا). يُعتقد أن النجوم الزائفة هي مجرات في مراحل تطورها المبكرة. وشأن المجرات النشطة، ظل مصدر السطوع الاستثنائي للنجوم الزائفة لغزا لبعض الوقت، إلى أن جرى الربط بين النجوم الزائفة وتكون الثقوب السوداء في مراكز المجرات حديثة التكون في الواقع، يُعتقد الآن على نطاق واسع أنه رغم أن المجرات النشطة والنجوم الزائفة تبدوان مختلفتين للغاية في نظرنا، فإنهما في الحقيقة جانبان مختلفان للظاهرة نفسها. فما النجوم الزائفة إلا مجرات نشطة بعيدة للغاية عنا. باختصار، الأدلة الداعمة لفكرة وجود الثقوب السوداء الفائقة الضخامة في مراكز المجرات؛ أدلة دامغة.

بعد أن تعرضنا للثقوب السوداء المجرية والنجمية، حري بنا الحديث عن نوع ثالث: «الثقوب السوداء الدقيقة». رأينا أنه إذا كانت كتلة النجم أقل من ضعفين إلى ثلاثة أضعاف كتلة الشمس، فإن جاذبيته لا تكون بالقوة الكافية بحيث ينضغط إلى ثقب أسود. ذلك، يمكن للنجوم الأقل ضخامة أن تصير ثقوباً سوداء إذا ما تعرضت لضغط ومع خارجي شديد بما يكفي. في عام 1971 اقترح ستيفن هوكينج أنه في ظروف الضغط والاضطراب الشديدين التي سادت في بواكير الانفجار العظيم ربما انضغطت التذبذات عالية الكثافة مكونة ثقوباً سوداء دقيقة. ربما كانت لهذه الثقوب كتلة لا تتجاوز مثلا كتلة جبل، وفي هذه الحالة لن يتجاوز أفق الحدث الخاص بها حجم البروتون. ربما توجد مثل هذه الأجسام في وقتنا الحالي، إلا أنه ما من دليل على وجودها.

وبالمثل ما من دليل على وجود الثقوب البيضاء»، التي هي مجرد احتمالية نظرية تسمح بها معادلة أينشتاين. فمثلما يكون الثقب الأسود منطقة من الفضاء لا يمكن لشيء الفكاك منها، يكون الثقب الأبيض منطقة لا يمكن للمرء أن يمنع خروج الأشياء منها! وثمة توقع جامح آخر يروق لكتّاب الخيال العلمي، هو «الثقب الدودي». تقضي هذه الفكرة بأنه بمجرد سقوط الجسم في ثقب أسود فإنه سيندفع عبر نفق إلى أن يخرج من ثقب أبيض. قد يكون هذا الثقب الأبيض في مكان آخر من الكون، أو في كون آخر كلية. ومجددًا نؤكد أنه ما من دليل على صحية أي من هذه الافتراضات. ثمة نقطة أخيرة تستحق الذكر بشأن الثقوب السوداء. ما الذي يحدث للثقب الأسود بعد تكونه؟ هل يظل موجودًا إلى الأبد؟ ستستمر الثقوب السوداء لفترة من الوقت في مراكمة المادة؛ وبذا تصير أضخم حجمًا. لكن لا بد من أن ينتهي هذا حين تبتلع كل المادة المتاحة لها. نحن نتوقع أن المطاف سينتهي بالثقب الأسود المجري وقد ابتلع كل النجوم في مجرته، وهي عملية ستستغرق 10²⁷ أعوام، اعتمادًا على الحجم المبدئي للمجرة. تنتمي  المجرات إلى عناقيد مجرية، كما هو الحال مع مجرتنا درب التبانة التي تنتمي – إضافة إلى ما يزيد عن الثلاثين مجرة - إلى (المجموعة المحلية للمجرات) تتحرك المجرات على نحو ثابت وترتبط بعضها مع بعض بفضل قوى الجاذبية المتبادلة، مثلما تكون مجموعة الكلاب المقيدة إلى وتد حرة في التجول لكن في حدود منطقة معينة. تطلق المجرات خلال تحركها الطاقة على صورة موجات جاذبية. هذا بدوره يعني أن كل المجرات التي يتكون منها أي عنقود مجري سينتهي بها الحال في ثقب أسود واحد. وبالنسبة إلى المجموعة المحلية من المفترض أن يستغرق هذا الأمر نحو 10³¹ أعوام.

في البداية كان يُظن أن هذه هي نهاية الحكاية. فعلى أي حال، لا شيء يسعه الفرار من الثقب الأسود، ولن يتبقى شيء ليدخل فيه. لكن في عام 1974 خرج ستيفن هوكينج بفكرة لامعة مفادها أن الثقوب السوداء يُفترض بها أن تسطع، وإن كان سطوعًا باهتًا للغاية، إلا أنها تشع طاقة على أي حال. تفسير هذا يأتينا من نظرية الكم، وهو ما يأخذنا بعيدًا عن نطاق هذا الكتاب الوجيز. لكن اسمحوا لي أن أستعرض باختصار كيف يحدث هذا.

ذكرنا من قبل أنه من منظور الفيزيائيين فإن الفضاء الخاوي – الفراغ – ليس خاويًا على الإطلاق بادئ ذي بدء، يمكنه أن ينحني). ووفق نظرية الكم، يُنتج الفراغ على نحو ثابت - وفي كل مكان - أزواجًا مما يطلق عليه «الجسيمات الافتراضية». هذه الأزواج تتكون من المادة والمادة المضادة، أو أزواج من الفوتونات (أي حزم من طاقة الضوء). تتطلب عملية إنتاج الجسيمات هذه طاقة من أجل إنتاج كتل السكون الخاصة بالجسيمات على سبيل المثال. لكن نظرية الكم تسمح بحدوث تذبذبات الطاقة، بمعنى أن الطاقة يمكن استعارتها، شريطة أن يتم إرجاعها على الفور. ومن ثم، تظهر هذه الأزواج من الجسيمات على نحو وجيز إلى الوجود، وسريعًا ما تعاود الاتحاد لتختفي من الوجود مجددًا. اقترح هوكينج أنه حين تحدث هذه العملية قرب أفق الحدث الخاص بثقب أسود، قد يسقط أحد الجسيمات الافتراضية داخل الثقب مطلقا طاقة جاذبية (تماما كما يحدث في حالة سقوط جسيم حقيقي في ثقب أسود). يطلق هذا طاقة قد تكون كافية لسداد الطاقة «المستعارة» دون أن يكون الجسيم الثاني مضطرا لسداد هذه الطاقة بنفسه. هذا الجسيم، أو الفوتون، الثاني الموجود خارج أفق الحدث مباشرة يكون حرا في الإفلات من الثقب الأسود مثلما يفعل أي. أو فوتون عادي. ومن ثم خلص جسیم هوكينج إلى أنه من المفترض أن تطلق الثقوب السوداء نوعًا ضعيفًا من الإشعاع. بعبارة أخرى: ليست الثقوب السوداء سوداء تمامًا. صار هذا الإشعاع معروفًا باسم «إشعاع هوكينج». وهو ضعيف للغاية لدرجة أنه لم يُرصد حتى الآن. فالثقب الأسود الذي تعادل كتلته كتلة الشمس، مثلا، سيطلق إشعاعًا تعادل حرارته 10^-7 درجات كلفينية فوق الصفر المطلق. ومع هذا، أغلب العلماء مقتنعون الآن بأن هذا هو السلوك التقليدي للثقوب السوداء. في هذه الحالة، يصير من الجلي أن الثقوب السوداء ستستمر في إطلاق الطاقة؛ ومن ثَم تفقد الكتلة. بمعنى آخر: ستتبخر الثقوب السوداء مثلما تتبخر بركة من الماء في يوم حار. وكلما كان الثقب الأسود أصغر، صار التفاوت في الانحناء في منطقته أكبر؛ ومن ثم صار من الأسهل على الجسيمات المكونة لأزواج الجسيمات الافتراضية أن تنفصل، بحيث يسقط أحد الجسيمين في الثقب الأسود بينما يفلت الآخر. ومن ثَم، كلما كان الثقب الأسود أصغر، كان إشعاع هوكينج أشد.

ما المصير النهائي إذن للثقب الأسود؟ من المتوقع أن تتبخر الثقوب السوداء ذات الكتلة النجمية في غضون 10⁶⁷ أعوام، فيما ستتبخر الثقوب ذات الكتلة المجرية في غضون 10⁹⁷ أعوام، أما الثقوب المتكونة من اندماج جميع أفراد العنقود المجري فستتبخر في غضون 10¹⁰⁶ أعوام.