تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Noncentral F-Distribution
المؤلف:
Patnaik, P. B.
المصدر:
"The Non-Central c_2- and F-Distributions and Their Applications." Biometrika 36
الجزء والصفحة:
...
10-4-2021
3351
+
-
20
Noncentral F-Distribution
The doubly noncentral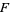 
-distribution describes the distribution 
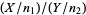for two independently distributed noncentral chi-squared variables 
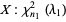and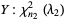 
(Scheffe 1959, Bulgren 1971). If 
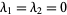, this becomes the usual (central) F-distribution, and if 
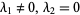, it becomes the singly noncentral 
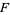-distribution. The case 
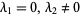gives a special case of the doubly noncentral distribution.
The probability density function of the doubly noncentral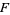 
-distribution is
 |
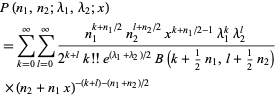(1) |
and the distribution function by
 |
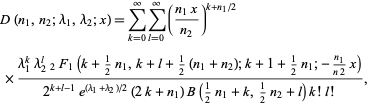(2) |
where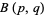 
is a beta function and 
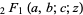is a hypergeometric function. The 
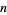th raw moment is given analytically as
 |
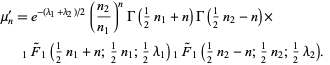(3) |
The singly noncentral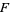 
-distribution is given by
 |
 |
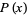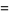![e^(-lambda/2+(lambdan_1x)/[2(n_2+n_1x)])n_1^(n_1/2)n_2^(n_2/2)x^(n_1/2-1)(n_2+n_1x)^(-(n_1+n_2)/2)(Gamma(1/2n_1)Gamma(1+1/2n_2)L_(n_2/2)^(n_1/2-1)(-(lambdan_1x)/(2(n_2+n_1x))))/(B(1/2n_1,1/2n_2)Gamma[1/2(n_1+n_2)])](https://mathworld.wolfram.com/images/equations/NoncentralF-Distribution/Inline16.gif) |
(4) |
 |
 |
 |
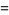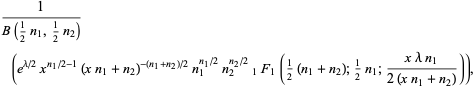(5) |
where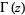 
is the gamma function, 
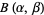is the beta function, and 
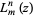is a generalized Laguerre polynomial. It is implemented in the Wolfram Language as NoncentralFRatioDistribution[n1, n2, lambda].
The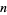 
th raw moment of the singly noncentral 
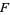-distribution is given analytically as
 |
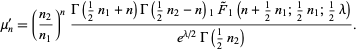(6) |
The first few raw moments are then
 |
 |
 |
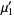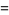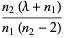(7) |
 |
 |
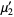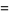![(n_2^2[lambda^2+2(n_1+2)lambda+n_1(n+1+2)])/(n_1^2(n_2-2)(n_2-4))](https://mathworld.wolfram.com/images/equations/NoncentralF-Distribution/Inline30.gif) |
(8) |
 |
 |
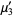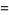![(n_2^3[lambda^3+3(n_1+4)lambda^2+3(n_1+2)(n_1+4)lambda+n_1(n_1+2)(n_1+4)])/(n_1^3(n_2-6)(n_2-4)(n_2-2))](https://mathworld.wolfram.com/images/equations/NoncentralF-Distribution/Inline33.gif) |
(9) |
 |
 |
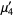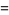![(n_2^4[lambda^4+4(n_1+6)lambda^3+6(n_1+4)(n_1+6)lambda^2+4(n_1+2)(n_1+4)(n_1+6)lambda+n_1(n_1+2)(n_1+4)(n_1+6)])/(n_1^4(n_2-8)(n_2-6)(n_2-4)(n_2-2)),](https://mathworld.wolfram.com/images/equations/NoncentralF-Distribution/Inline36.gif) |
(10) |
and the first few central moments are
 |
 |
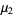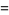![(2n_2^2[lambda^2+2(n_1+n_2-2)lambda+n_1(n_1+n_2-2)])/(n_1^2(n_2-2)^2(n_2-4))](https://mathworld.wolfram.com/images/equations/NoncentralF-Distribution/Inline39.gif) |
(11) |
 |
 |
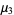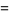![(8n_2^3[2lambda^3+6(n_1+n_2-2)lambda^2+3(n_1+n_2-2)(2n_1+n_2+2)lambda+n_1(n_1+n_2-2)(2n_1+n_2-2)])/(n_1^3(n_2-2)^3(n_2-4)(n_2-6)).](https://mathworld.wolfram.com/images/equations/NoncentralF-Distribution/Inline42.gif) |
(12) |
The mean and variance are therefore given by
 |
 |
 |
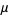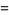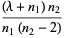(13) |
 |
 |
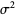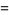![(n_2^2[lambda^2+(2n_1+4)lambda+n_1(n_1+2)])/(n_1^2(n_2-4)(n_2-2)^2).](https://mathworld.wolfram.com/images/equations/NoncentralF-Distribution/Inline48.gif) |
(14) |
REFERENCES:
Patnaik, P. B. "The Non-Central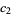 
- and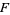 
-Distributions and Their Applications." Biometrika 36, 202-232, 1949.
Bulgren, W. G. "On Representations of the Doubly Non-Central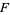 
Distribution." J. Amer. Stat. Assoc. 66, 184, 1971.
Scheffé, H. The Analysis of Variance. New York: Wiley, pp. 135 and 415, 1959.
Stuart, A.; and Ord, J. K. Kendall's Advanced Theory of Statistics, Vol. 2A: Classical Inference & the Linear Model, 6th ed. New York: Oxford University Press, p. 893, 1999.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
