Buffon's Needle Problem

Buffon's needle problem asks to find the probability that a needle of length 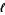 will land on a line, given a floor with equally spaced parallel lines a distance  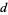apart. The problem was first posed by the French naturalist Buffon in 1733 (Buffon 1733, pp. 43-45), and reproduced with solution by Buffon in 1777 (Buffon 1777, pp. 100-104).

Define the size parameter  by

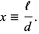(1)

For a short needle (i.e., one shorter than the distance between two lines, so that 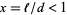), the probability  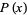that the needle falls on a line is

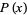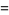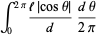			(2)
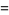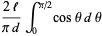			(3)
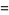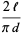			(4)
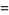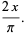			(5)

For 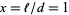, this therefore becomes

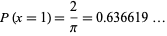(6)

(OEIS A060294).

For a long needle (i.e., one longer than the distance between two lines so that 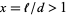), the probability that it intersects at least one line is the slightly more complicated expression

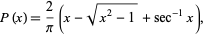(7)

where (Uspensky 1937, pp. 252 and 258; Kunkel).

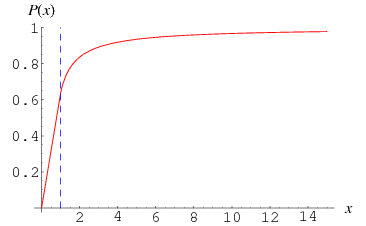
Writing

(8)

then gives the plot illustrated above. The above can be derived by noting that

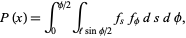(9)

where

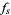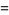			(10)
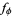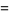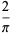			(11)

are the probability functions for the distance 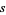 of the needle's midpoint  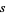from the nearest line and the angle  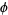formed by the needle and the lines, intersection takes place when 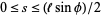, and 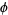 can be restricted to  by symmetry.

Let 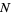 be the number of line crossings by  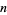tosses of a short needle with size parameter . Then 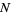 has a binomial distribution with parameters  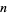and 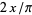. A point estimator for  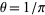is given by

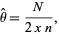(12)

which is both a uniformly minimum variance unbiased estimator and a maximum likelihood estimator (Perlman and Wishura 1975) with variance

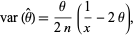(13)

which, in the case 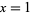, gives

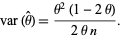(14)

The estimat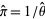or  for 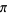 is known as Buffon's estimator and is an asymptotically unbiased estimator given by

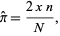(15)

where 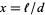,  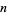is the number of throws, and  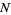is the number of line crossings. It has asymptotic variance

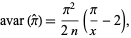(16)

which, for the case 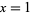, becomes

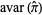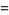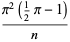			(17)
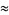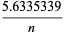			(18)

(OEIS A114598; Mantel 1953; Solomon 1978, p. 7).

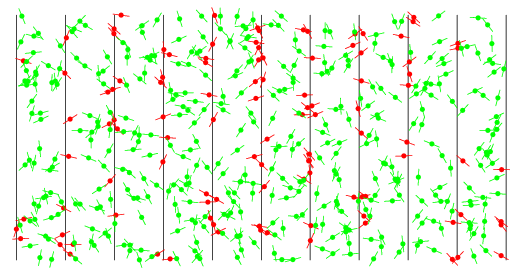
The above figure shows the result of 500 tosses of a needle of length parameter 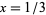, where needles crossing a line are shown in red and those missing are shown in green. 107 of the tosses cross a line, giving .

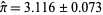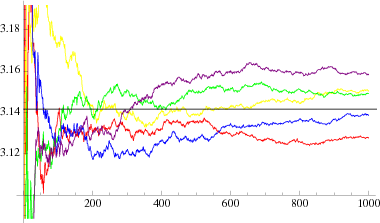
Several attempts have been made to experimentally determine 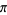 by needle-tossing.  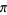calculated from five independent series of tosses of a (short) needle are illustrated above for one million tosses in each trial 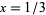. For a discussion of the relevant statistics and a critical analysis of one of the more accurate (and least believable) needle-tossings, see Badger (1994). Uspensky (1937, pp. 112-113) discusses experiments conducted with 2520, 3204, and 5000 trials.

The problem can be extended to a "needle" in the shape of a convex polygon with generalized diameter less than 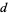. The probability that the boundary of the polygon will intersect one of the lines is given by

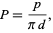(19)

where 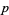 is the perimeter of the polygon (Uspensky 1937, p. 253; Solomon 1978, p. 18).

A further generalization obtained by throwing a needle on a board ruled with two sets of perpendicular lines is called the Buffon-Laplace needle problem.

REFERENCES:

Badger, L. "Lazzarini's Lucky Approximation of 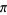." Math. Mag. 67, 83-91, 1994.

Bogomolny, A. "Buffon's Noodle." http://www.cut-the-knot.org/Curriculum/Probability/Buffon.shtml.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 139, 2003.

Buffon, G. Editor's note concerning a lecture given 1733 by Mr. Le Clerc de Buffon to the Royal Academy of Sciences in Paris. Histoire de l'Acad. Roy. des Sci., pp. 43-45, 1733.

Buffon, G. "Essai d'arithmétique morale." Histoire naturelle, générale er particulière, Supplément 4, 46-123, 1777.

Diaconis, P. "Buffon's Needle Problem with a Long Needle." J. Appl. Prob. 13, 614-618, 1976.

Dörrie, H. "Buffon's Needle Problem." §18 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 73-77, 1965.

Edelman, A. and Kostlan, E. "How Many Zeros of a Random Polynomial are Real?" Bull. Amer. Math. Soc. 32, 1-37, 1995.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, p. 209, 1998.

Isaac, R. The Pleasures of Probability. New York: Springer-Verlag, 1995.

Kendall, M. G. and Moran, P. A. P. Geometrical Probability. New York: Hafner, 1963.

Klain, Daniel A. and Rota, G.-C. Introduction to Geometric Probability. New York: Cambridge University Press, 1997.

Kraitchik, M. "The Needle Problem." §6.14 in Mathematical Recreations. New York: W. W. Norton, p. 132, 1942.

Kunkel, P. "Buffon's Needle." http://whistleralley.com/buffon/buffon.htm.

Mantel, L. "An Extension of the Buffon Needle Problem." Ann. Math. Stat. 24, 674-677, 1953.

Morton, R. A. "The Expected Number and Angle of Intersections Between Random Curves in a Plane." J. Appl. Prob. 3, 559-562, 1966.

Perlman, M. and Wichura, M. "Sharpening Buffon's Needle." Amer. Stat. 20, 157-163, 1975.

Santaló, L. A. Integral Geometry and Geometric Probability. Reading, MA: Addison-Wesley, 1976.

Schuster, E. F. "Buffon's Needle Experiment." Amer. Math. Monthly 81, 26-29, 1974.

Sloane, N. J. A. Sequences A060294 and A114598 in "The On-Line Encyclopedia of Integer Sequences."

Solomon, H. "Buffon Needle Problem, Extensions, and Estimation of 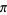." Ch. 1 in Geometric Probability. Philadelphia, PA: SIAM, pp. 1-24, 1978.

Stoka, M. "Problems of Buffon Type for Convex Test Bodies." Conf. Semin. Mat. Univ. Bari, No. 268, 1-17, 1998.

Uspensky, J. V. "Buffon's Needle Problem," "Extension of Buffon's Problem," and "Second Solution of Buffon's Problem." §12.14-12.16 in Introduction to Mathematical Probability. New York: McGraw-Hill, pp. 112-115, 251-255, and 258, 1937.

Wegert, E. and Trefethen, L. N. "From the Buffon Needle Problem to the Kreiss Matrix Theorem." Amer. Math. Monthly 101, 132-139, 1994.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 53, 1986.

Wood, G. R. and Robertson, J. M. "Buffon Got It Straight." Stat. Prob. Lett. 37, 415-421, 1998.