Moment-Generating Function
المؤلف:
Kenney, J. F. and Keeping, E. S.
المصدر:
"Moment-Generating and Characteristic Functions," "Some Examples of Moment-Generating Functions," and "Uniqueness Theorem for Characteristic Functions
الجزء والصفحة:
...
22-2-2021
1744
Moment-Generating Function
Given a random variable 
and a probability density function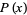 
, if there exists an 
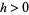such that
 |
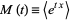(1)
|
for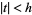 
, where 
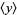denotes the expectation value of 
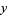, then 
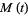is called the moment-generating function.
For a continuous distribution,
where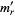 
is the 
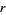th raw moment.
For independent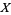 
and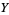 
, the moment-generating function satisfies
If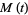 
is differentiable at zero, then the 
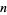th moments about the origin are given by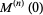 
The mean and variance are therefore
It is also true that
 |
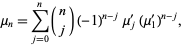(17)
|
where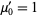 
and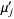 
is the 
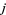th raw moment.
It is sometimes simpler to work with the logarithm of the moment-generating function, which is also called the cumulant-generating function, and is defined by
But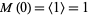 
, so
REFERENCES:
Kenney, J. F. and Keeping, E. S. "Moment-Generating and Characteristic Functions," "Some Examples of Moment-Generating Functions," and "Uniqueness Theorem for Characteristic Functions." §4.6-4.8 in Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 72-77, 1951.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
