Kendall Operator

The operator 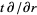 that can be used to derive multivariate formulas for moments and cumulants from corresponding univariate formulas.

For example, to derive the expression for the multivariate central moments 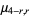 in terms of multivariate cumulants, begin with

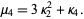(1)

Now rewrite each variable 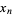 as 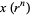 to obtain

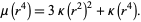(2)

Now differentiate each side with respect to 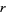, where

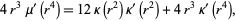(3)

and wherever there is a term with a derivative 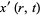, remove the derivative and replace the argument with  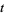times itself, so

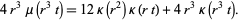(4)

Now set any 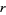s appearing as coefficients to 1, so

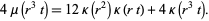(5)

Dividing through by 4 gives

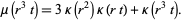(6)

Finally, set any coefficients powers of 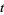 appearing as term coefficients to 1 and interpret the resulting term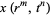s  as 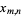, so that the above gives

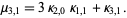(7)

This procedure can be repeated up to 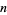 times, where  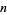is the subscript of the univariate case.

Iterating the above procedure gives

			(8)
			(9)
			(10)
			(11)
			(12)

giving the identities

			(13)
			(14)
			(15)
			(16)
			(17)

REFERENCES:

Kendall, M. G. "The Derivation of Multivariate Sampling Formulae from Univariate Formulae by Symbolic Operation." Ann. Eugenics 10, 392-402, 1940.

Stuart, A.; and Ord, J. K. Kendall's Advanced Theory of Statistics, Vol. 1: Distribution Theory, 6th ed. New York: Oxford University Press, 1998.