Covariance
المؤلف:
Snedecor, G. W. and Cochran, W. G
المصدر:
Statistical Methods, 7th ed. Ames, IA: Iowa State Press
الجزء والصفحة:
...
19-2-2021
1904
Covariance
Covariance provides a measure of the strength of the correlation between two or more sets of random variates. The covariance for two random variates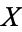 
and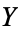 
, each with sample size 
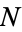, is defined by the expectation value
where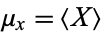 
and 
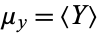are the respective means, which can be written out explicitly as
 |
(3)
|
For uncorrelated variates,
 |
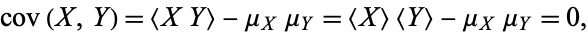(4)
|
so the covariance is zero. However, if the variables are correlated in some way, then their covariance will be nonzero. In fact, if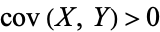 
, then 
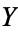tends to increase as 
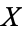increases, and if 
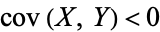, then 
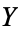tends to decrease as 
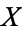increases. Note that while statistically independent variables are always uncorrelated, the converse is not necessarily true.
In the special case of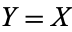 
,
so the covariance reduces to the usual variance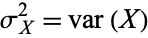 
. This motivates the use of the symbol 
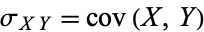, which then provides a consistent way of denoting the variance as 
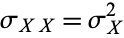, where 
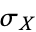is the standard deviation.
The derived quantity
is called statistical correlation of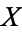 
and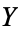 
.
The covariance is especially useful when looking at the variance of the sum of two random variates, since
 |
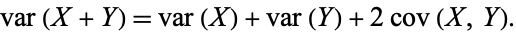(9)
|
The covariance is symmetric by definition since
 |
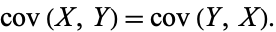(10)
|
Given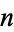 
random variates denoted 
, ..., 
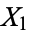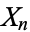, the covariance 
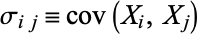of 
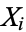and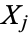 
is defined by
where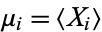 
and 
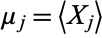are the means of 
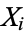and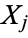 
, respectively. The matrix 
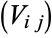of the quantities 
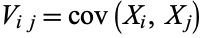is called the covariance matrix.
The covariance obeys the identities
By induction, it therefore follows that
REFERENCES:
Snedecor, G. W. and Cochran, W. G. Statistical Methods, 7th ed. Ames, IA: Iowa State Press, p. 180, 1980.
Spiegel, M. R. Theory and Problems of Probability and Statistics, 2nd ed. New York: McGraw-Hill, p. 298, 1992.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
