3 - 5 - 7 أسلوب شبكات النقل Transportation Network Method

لقد ذكرنا آنفا أن تكاليف نقل المواد الخام إلى المصنع، ونقل المواد تامة الصنع إلى مراكز البيع أو التخزين تعد من العناصر المهمة التي تُؤخذ في الحسبان عند اختيار موقع المصنع، ولما كانت تلك التكاليف تؤثر في الكلفة النهائية للمنتوج، فان الإدارة تحاول تحديد المنتجات التي سيضطلع بإنتاجها معمل ما في منطقة معينة، وأيضاً تحديد المناطق التي ستُنقل إليها المنتجات تامة الصنع لتحقيق اقل تكاليف ممكنة للتنقل.

ويعد أسلوب شبكات النقل من الأدوات المفيدة في حل مسائل اختيار موقع لمصنع واحد لو لعدة مصانع، ويستمد هذا الأسلوب تسميته من معالجته لمشاكل نقل منتجات من مصانع متعددة إلى مناطق متعددة بهدف تخفيض تكاليف التنقل إلى أدنى حد ممكن وتعظيم الأرباح المتحققة عن ذلك، ويجري ذلك ضمن قيود الطاقة الإنتاجية المُتاحة للمصانع والطلب على المنتجات ويقوم هذا الأسلوب على الافتراضات الاتية :

• ان الهدف الرئيس هو تخفيض تكاليف النقل الى ادنى حد ممكن .

• أن تكاليف الإنتاج و النقل ثابتة لا تتغير وتُحسب كدالة لعدد الوحدات  المنقولة.

• أن الطلب والإنتاج يمكن التعبير عنهما بوحدات قياس متشابهة.

• أن الوحدات المُنتجة في المصانع متشابهة بغض النظر عن الموقع الذي أنتجت فيه.

• أن مجموع الطاقة الإنتاجية للمصانع يساوي مجموع الطلب للمناطق و إذا حدث أن الطاقة الإنتاجية تفوق الطلب فيتم خلق منطقة وهمية لاستهلاك الزيادة في الإنتاج وبخلافه يتم خلق معمل وهمي لسد الطلب.

ولتوضيح كيفية تطبيق أسلوب النقل نستخدم مثالاً حول توزيع منتجات عدد من المعامل إلى عدد من المناطق الاستهلاكية ثم نقدم فيما بعد مثالاً أخراً لتوضيح كيفية استخدام هذا الأسلوب في اختيار موقع المصنع.

مثال (7-3): تمتلك إحدى الشركات أربعة مصانع للسجاد الصناعي (قياس 3×2 قدم) وتقوم هذه المصانع بتوزيع منتجاتها على أربعة مخازن في العراق وقد لاحظت الإدارة ارتفاع تكاليف النقل للسجاد من المصانع إلى المخازن وحدوث شحة في أحد المخازن واختناق في مخازن أخرى فما هو التوزيع الأمثل الذي نحصل عليه باستخدام شبكة النقل وبيانات الإنتاج والطلب والتكاليف الاتية ؟

ولإيجاد الحل الأمثل لهذه المسالة فأن هناك ثلاث خطوات يجب القيام بها بالتتابع وهي: أعداد شبكة النقل، إيجاد الحل الأولي، وإيجاد الحل الأمثل. وسنوضح فيما يأتي كل واحدة من هذه الخطوات بالتفصيل : 

الخطوة الأولى : أعداد شبكة النقل 

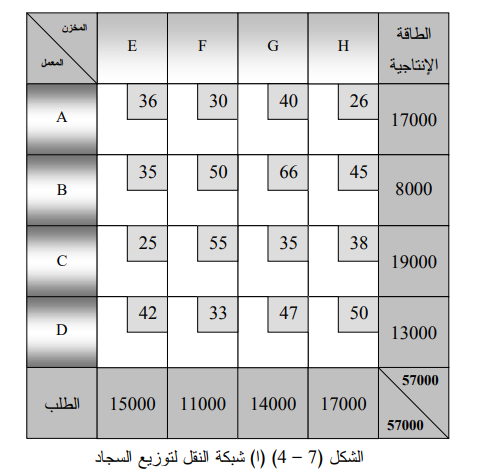
يوضح الشكل (7 - 4)(أ) شبكة النقل لهذه المسالة وتظهر في هذه الشبكة الطاقة الإنتاجية (جانب التجهيز) للمعامل على جهة اليمين بينما تظهر حاجة المخازن (جانب الطلب) في أسفل الشبكة، ويلاحظ أيضا أن جانبي الطلب والتجهيز متساويان فضلاً عن ذلك فأن تكاليف النقل من المصنع إلى المخزن تظهر داخل مربع صغير في الخلية الخاصة بها.

الخطوة الثانية : إيجاد الحل الأولي

يعد الحل الأولي لشبكة النقل نقطة البداية للوصول إلى الحل الأمثل وهناك عدة طرائق لأعداد الحل الأولي مثل أسلوب الكلفة الأصغرية Least -Cost Method. وأسلوب فوغال التقريبي  Vogel ' s    ((VAM Approximation Method وأسلوب الزاوية الشمالية الغربية ^{* *}North - West Corner ( NMC ) Method . و سوف نستخدم هنا أسلوب الزاوية الشمالية الغربية نظراً لبساطته. ولإيجاد الحل الأولي بموجب هذا الأسلوب فأننا نبدأ من الصف الأول للشبكة ومن الخلية الأولى من جهة اليسار في الصف ونقوم بتخصيص أكبر كمية ممكنة من إنتاج معمل (A) إلى مخزن (E) وهذه الكمية هي 15000 وحدة وليس بالإمكان تخصيص كمية أكبر لأنها تصل إلى حدود طلب مخزن (E) والبالغ 15000 وحدة والذي يشكل عقبة أمام تخصيص كمية أكبر من 15000. ولما كان إنتاج معمل (A) يبلغ 17000 وحدة فأن هناك 2000 وحدة يمكن توزيعها إلى مخزن (F) وبهذا يكون معمل (A) قد وزع كل إنتاجه وكما يظهر في الشكل (7-4) (ب). بعد ذلك ننتقل الى الصف الثاني في الشبكة ونلاحظ أن معمل (B) ينتج 8000 وحدة و أن مخزن (F) قد تسلم 2000 وحدة وأنه بحاجة إلى 9000 وحدة أخرى ،فلذلك يخصص جميع إنتاج معمل (B) إلى مخزن (F) فيصبح مجموع ما تسلمه مخزن F) ) 10000وحدة وأنه ما زال بحاجة إلى 1000 وحدة أخرى فتُؤخذ هذه بدورها من معمل (C). ونستمر بهذه الطريقة حتى يتم توزيع إنتاج المعامل على المخازن بحيث تكون مجاميع الكميات المخصصة في الصفوف الأفقية والعمودية في الشبكة مساوية إلى المجاميع التي تقابلها على جهة اليمين واسفل الشبكة وكما يظهر في الشكل (7 - 4) - (ب).

وبضرب كلفة النقل المقترنة بكل مصنع ومخزن بالكمية المخصصة لها ، نحصل على الكلية للحل الأولي وكما يأتي :

الخطوة الثالثة : إيجاد الحل الأمثل بطريقة القفز على الصخور Stepping Stone Method :

لإيجاد الحل الأمثل والكلفة الأصغرية للنقل نحاول أن نغير في الكميات المخصصة من المعامل إلى المخازن وذلك لتحقيق وفورات في تكاليف النقل، ولكي يتم تطبيق طريقة القفز علي الصخور يجب أن نتأكد أولاً من أن عدد الخلايا المشغولة في الحل الأولي مساويا الناتج العلاقة الآتية :

عدد الخلايا المشغولة = عدد الصفوف + عدد الأعمدة - 1

Number of Occupied Cells = m+n-1                

وهذا يعني أن الحل الأولي لمثالنا يجب أن يحتوي على 7 خلايا مشغولة (4+4-1=7) وهو ما موجود فعلاً ، أن تطوير الحل الأولي للوصول الى الحل الأمثل يتطلب اختبار كل خلية غير مشغولة لمعرفة إمكانية جدوى إجراء المناقلة في الكميات المخصصة.

وان اختبار كل خلية غير مخصص لها يتم وفقاً للخطوات الآتية:         

1 ـ حصر جميع الخلايا غير المشغولة (Unoccupied Cells) ورسم مسار مغلق (Closed Path) لكل خلية لغرض تقييمها.                        

2- لرسم مسار مغلق لخلية غير مشغولة، ابدأ بتلك الخلية مروراً بخلايا مشغولة حالياً بواسطة خطوط أفقية وعمودية فقط رجوعاً في نهاية المسار الى نفس الخلية غير المشغولة.     

3 - ابدأ بوضع وحدة واحدة بعلامة موجبة (1+) في الخلية غير المشغولة، ثم ضع قيم بإشارات سالبة (1-) و إشارات موجبة (1+) بالتعاقب لكل خلية مشغولة تشكل زاوية فقط في المسار المغلق.            

4- احسب دليل التحسين (I-Improvement Index) لكل مسار مغلق وذلك بجمع أرقام تكاليف نقل الوحدة في كل خلية تحمل علامة موجبة ومن ثم إطرح منها  تكاليف نقل الوحدة في كل خلية تحمل علامة سالبة.

5- اذا كانت قيم جميع أدلة التحسين أكبر من أو تساوي صفراً، فإن ذلك يعني قد تم الوصول إلى الحل الأمثل. وبعكسه فإن هناك إمكانية لتحسين الحل الحالي وتقليل التكاليف الكلية للنقل باختيار المسار الذي يقترن بأكبر قيمة سالبة لغرض اختباره .  

وبتطبيق هذه الخطوات نجد أن المسارات المغلقة للخلايا غير المشغولة التي تقترن أدلة تحسينها بقيم سالبة هي : 

سيتم اختيار المسار المغلق CE لأن دليل التحسين فيه يقترن بأكبر قيمة   سالبة (36ــ) وذلك لغرض اختبار امكانية تأثيره في تخفيض التكاليف الكلية للنقل. فلو قمنا بإضافة أي كمية إلى هذه الخلية فأن الكميات في الخلايا الثلاث الأخرى للمسار يجب أن تتغير (تزيد أو تنقص) بنفس الكمية لكي تبقى المجاميع الأفقية للصفوف والعمودية للأعمدة مساوية الى مجموع الخلايا المقترنة بها. ولكن قبل أن نُغير في الكميات يجب أن نتوقف على صلاحية اجراء النقلة بين هذه الخلايا. وللوصول إلى ذلك نجرب بتغيير وحدة واحدة بين هذه الخلايا بمقدار (+1) فإذا كان هناك توفير في تكاليف النقل فلا بأس من إجراء النقلة ونوضح ذلك كما يأتي:

ويضرب كمية النقل بين هذه الخلايا بكلفة النقل في كل خلية تتوصل الى ان تغيير وحدة واحدة بين هذه الخلايا يوفر 36 دولار/ وحدة منقولة ضمن هذا المسار، أي :

1 × 25 ــ 1 × 55  + 1 × 30 ــ 1 × 36 = ــ 36 دولار*    

وبما أن هدفنا هو تخفيض تكاليف النقل، لذلك سنحاول نقل اكبر كمية ممكنة بين هذه الخلايا، وهذه الكمية تبلغ 1000 وحدة وهي اقصى ما يمكن طرحه من الخلايا التي تحمل علامة سالبة، ولتحقيق ذلك نضيف 1000 وحدة الى كل خلية تحمل علامة موجبة، وتطرح 1000 وحدة من كل خلية تحمل علامة سالبة. فنحصل على توزيع جديد لهذه الخلايا كما يأتي :

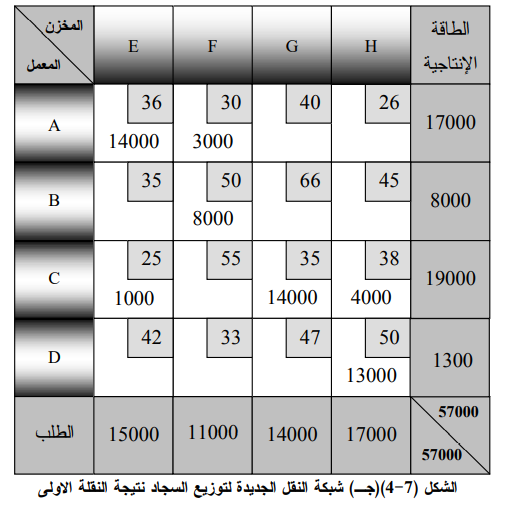
ويوضح الشكل (4 7) (ج) التوزيع الجديد لإنتاج المعامل على المخازن بعد أجراء النقلة الأولى، ولمعرفة الكلفة الكلية بعد هذه النقلة فأننا نضرب مقدار التوفير الذي تحقق عن كل وحدة في الكمية التي نُقلت بين الخلايا، ثم نُطرح الناتج من آخر حل توصلنا إليه (أي كلفة الحل الأولي في هذه الحالة) : 

36 × 1000 = 36000 دولار

2347000 ــ 36000 = 2311000 دولار نتيجة النقلة الاولى .

بعد تخفيض كلفة النقل في المحاولة الاولى ، نحاول إجراء نقلات الى الخلايا الاخرى الشاغرة في شبكة النقل على امل تخفيض التكاليف مجدداً وذلك باتباع نفس الخطوات السابقة لاختيار الخلايا غير المشغولة ، ونختار هذه المرة الخلية BH لاقتران مسارها المغلق بأكبر قيمة سالبة   (-24) وكما يأتي :

نجرب الآن صلاحية النقل وذلك بإضافة او طرح وحدة واحدة بين هذه الخلايا وكما يأتي :
 

وبما ان النتيجة سالبة فذلك يعني ان إجراء تغيير بين هذه الخلايا سيؤدي الى تخفيض تكاليف النقل بمقدار 24 دولار / وحدة ، وبما ان اصغر كمية تظهر في الخلايا التي تحمل علامة سالبة هي 4000 لذلك سنضيف 4000 وحدة لكل خلية تحمل علامة موجبة ونطرح 4000 وحدة من كل خلية تحمل علامة سالبة وكما موضح ادناه :

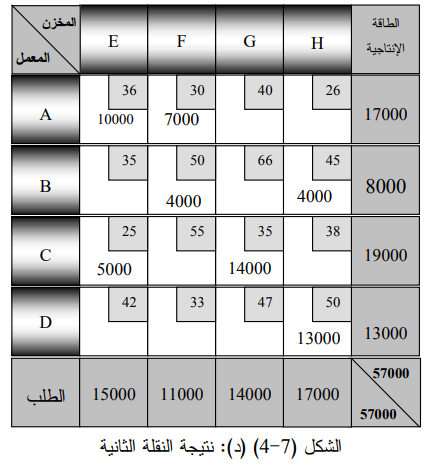
والشكل (7-4) (د) يوضح شبكة النقل بعد النقلة الثانية ، وبطرح مقدار التوفير 96000 ( 4000 ×24 ) من آخر كلفة نقل توصلنا لها وهي 2311000 دولار، نتوصل الى كلفة الحل المقترن بالنقلة الثانية كما يأتي : 2311000 ــ (24 × 4000) = 2215000 دولار ، والشكل (7-4) (د) يوضح نتيجة النقلة الثانية :

نقوم باختبار الخلايا غير المشغولة الجديدة في الشكل (7-4)(د) لغرض معرفة فيما اذا كان الحل بعد إجراء النقلة الثانية هو الحل الامثل ام لا . وقد تبين أنه لا يمثل الحل الامثل لوجود أدلة تحسين سالبة للخلايا غير المشغولة AG = -6  ، BE = -21   ،  DE = -16  ، DF = -22 ، DG = -24  ، لذلك نجرب الخلية غير المشغولة DG لأن مسارها المغلق يقترن باكبر قيمة سالبة   -24 وكالآتي :

طالما ان ادنى كمية في الخلايا التي تحمل علامة سالبة تبلغ (4000) وحدة ، ولغرض إكمال الحل بموجب هذه النقلة نضيف (4000) وحدة الى كل خلية تحمل علامة موجبة ونطرح (4000) وحدة من كل خلية تحمل علامة سالبة وكما مبين ادناه :

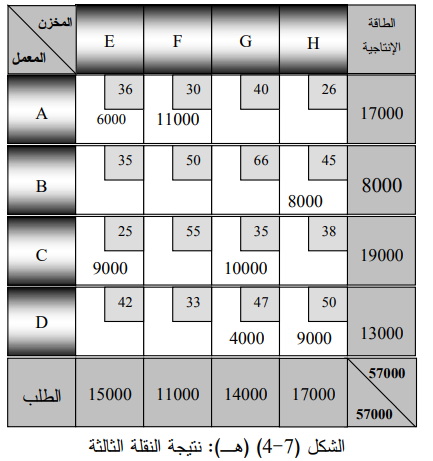
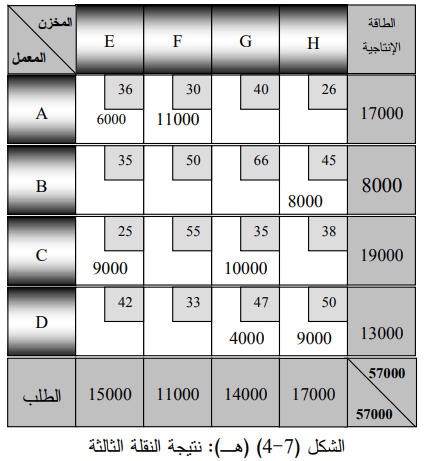
والشكل (4-7) (هـ) يوضح شبكة النقل بعد النقلة الثالثة ، وبطرح مقدار التوفير 96000 (4000 ×24) من آخر كلفة نقل توصلنا لها وهي 2215000 دولار ، نتوصل الى كلفة الحل المقترن بالنقلة الثالثة كما يأتي: 2215000 ــ (24 × 4000) = 2115000 دولار .

ونستمر بإجراء النقلات بنفس الطريقة حتى نصل الى الحل الأمثل الذي يظهر (4-7) (ز) والذي تبلغ كلفته الكلية 1774000 دولار ويبلغ مقدار التوفير بين الحل الاولي والحل الأمثل 573000 دولار وذلك بفضل استخدام تحليل شبكات النقل  

ــــــــــــــــــــــــــــــــ

**وهناك طريقتان توصلان الى الحل الامثل وهما طريقة القفز على الصخور Stepping Stone Method  وطريقة التوزيع المعدل Modified Distribution(MODI) Method  .

*اذا ظهرت النتيجة موجبة فليس من الاقتصادي إجراء التغيير بين هذه الخلايا لأن ذلك سيرفع التكاليف بمقدار 36 دولار / وحدة وهو عكس ما نهدف اليه .