
Score Function
 المؤلف:
Rodriguez, G.
المؤلف:
Rodriguez, G.
 المصدر:
"Lecture Notes on Generalized Linear Models." 2007. https://data.princeton.edu/wws509/notes/.
المصدر:
"Lecture Notes on Generalized Linear Models." 2007. https://data.princeton.edu/wws509/notes/.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 10-2-2021
10-2-2021
 1522
1522
Score Function
The score function 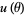 is the partial derivativeof the log-likelihood function
is the partial derivativeof the log-likelihood function 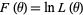 , where
, where 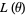 is the standard likelihood function.
is the standard likelihood function.
Defining the likelihood function
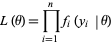 |
(1)
|
shows that
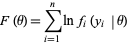 |
(2)
|
and thus that
Using the above formulation of 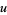 , one can easily compute various statistical measurements associated with
, one can easily compute various statistical measurements associated with 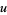 . For example, the mean
. For example, the mean 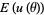 can be shown to equal zero while the variance is precisely the Fisher information matrix. The score function has extensive uses in many areas of mathematics, both pure and applied, and is a key component of the field of likelihood theory.
can be shown to equal zero while the variance is precisely the Fisher information matrix. The score function has extensive uses in many areas of mathematics, both pure and applied, and is a key component of the field of likelihood theory.
REFERENCES:
Rodriguez, G. "Lecture Notes on Generalized Linear Models." 2007. https://data.princeton.edu/wws509/notes/.
Sun, D. and Xiao, F. "Likelihood Theory with Score Function." 2013. https://www.stats.uwo.ca/faculty/bellhouse/Likelihood_Theory_with_Score_Function.pdf
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


