المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Logarithmically Concave Sequence |
 874
 02:10 صباحاً
date: 1-11-2020 |
Author : Levit, V. E. and Mandrescu, E. 
Book or Source : "The Independence Polynomial of a Graph--A Survey." In Proceedings of the 1st International Conference on Algebraic Informatics. Held in... 
Page and Part : ...|
Read More
Date: 28-9-2020
961
Date: 8-3-2020
906
Date: 19-9-2020
846
|
A finite sequence of real numbers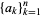 
is said to be logarithmically concave (or log-concave) if
 |
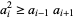holds for every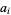 
with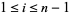 
.
A logarithmically concave sequence of positive numbers is also unimodal.
If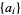 
and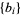 
are two positive log-concave sequences of the same length, then 
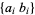is also log-concave. In addition, if the polynomial 
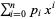has all its zeros real, then the sequence 
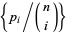is log-concave (Levit and Mandrescu 2005).
An example of a logarithmically concave sequence is the sequence of binomial coefficients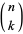 
for fixed 
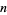and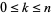 
.
REFERENCES:
Levit, V. E. and Mandrescu, E. "The Independence Polynomial of a Graph--A Survey." In Proceedings of the 1st International Conference on Algebraic Informatics. Held in Thessaloniki, October 20-23, 2005 (Ed. S. Bozapalidis, A. Kalampakas, and G. Rahonis). Thessaloniki, Greece: Aristotle Univ., pp. 233-254, 2005.
|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|
