Fredholm Integral Equation of the Second Kind

An integral equation of the form

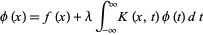(1)

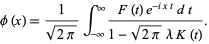(2)

The solution to a general Fredholm integral equation of the second kind is called an integral equation Neumann series.

A Fredholm integral equation of the second kind with separable integral kernel may be solved as follows:

			(3)
			(4)
			(5)

where

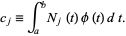(6)

Now multiply both sides of (◇) by 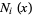 and integrate over .

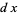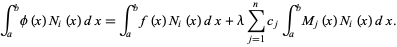(7)

By (◇), the first term is just 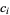. Now define

			(8)
			(9)

so (◇) becomes

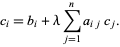(10)

Writing this in matrix form,

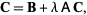(11)

so

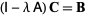(12)

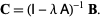(13)

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 865, 1985.

Baker, C. T. H. The Numerical Treatment of Integral Equations. Oxford, England: Clarendon Press, pp. 358-360, 1977.

Pearson, C. E. Handbook of Applied Mathematics. New York: Van Nostrand, 1990.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Fredholm Equations of the Second Kind." §18.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 782-785, 1992.