
Wave Equation--Rectangle
 المؤلف:
المرجع الالكتروني للمعلوماتيه
المؤلف:
المرجع الالكتروني للمعلوماتيه
 المصدر:
المرجع الالكتروني للمعلوماتيه
المصدر:
المرجع الالكتروني للمعلوماتيه
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-7-2018
25-7-2018
 2997
2997
Wave Equation--Rectangle
To find the motion of a rectangular membrane with sides of length 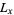 and
and 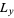 (in the absence of gravity), use the two-dimensional wave equation
(in the absence of gravity), use the two-dimensional wave equation
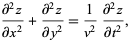 |
(1)
|
where 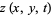 is the vertical displacement of a point on the membrane at position (
is the vertical displacement of a point on the membrane at position (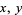 ) and time
) and time 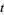 . Use separation of variables to look for solutions of the form
. Use separation of variables to look for solutions of the form
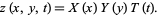 |
(2)
|
Plugging (2) into (1) gives
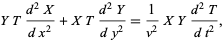 |
(3)
|
where the partial derivatives have now become complete derivatives. Multiplying (3) by 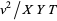 gives
gives
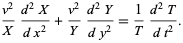 |
(4)
|
The left and right sides must both be equal to a constant, so we can separate the equation by writing the right side as
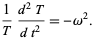 |
(5)
|
This has solution
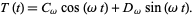 |
(6)
|
Plugging (5) back into (◇),
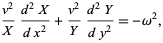 |
(7)
|
which we can rewrite as
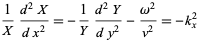 |
(8)
|
since the left and right sides again must both be equal to a constant. We can now separate out the 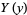 equation
equation
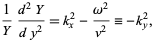 |
(9)
|
where we have defined a new constant 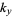 satisfying
satisfying
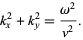 |
(10)
|
Equations (◇) and (◇) have solutions
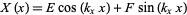 |
(11)
|
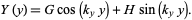 |
(12)
|
We now apply the boundary conditions to (11) and (12). The conditions 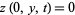 and
and 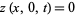 mean that
mean that
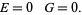 |
(13)
|
Similarly, the conditions 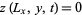 and
and 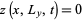 give
give 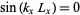 and
and 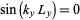 , so
, so 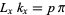 and
and 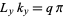 , where
, where 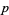 and
and 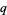 are integers. Solving for the allowed values of
are integers. Solving for the allowed values of 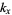 and
and 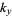 then gives
then gives
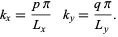 |
(14)
|
Plugging (◇), (◇), (◇), (◇), and (14) back into (◇) gives the solution for particular values of 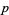 and
and 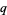 ,
,
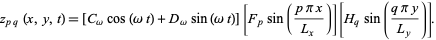 |
(15)
|
Lumping the constants together by writing 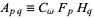 (we can do this since
(we can do this since  is a function of
is a function of  and
and 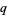 , so
, so 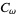 can be written as
can be written as 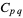 ) and
) and 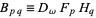 , we obtain
, we obtain
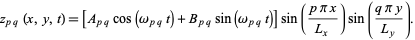 |
(16)
|
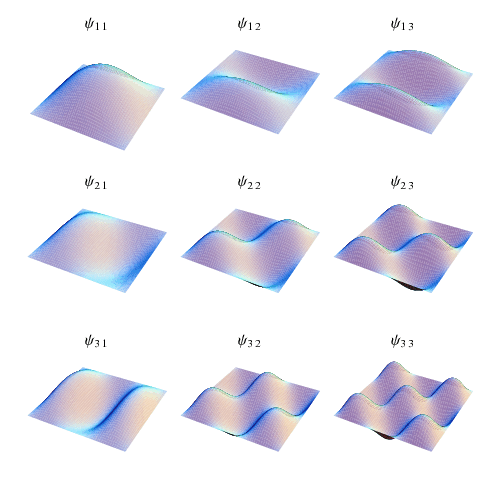
Plots of the spatial part for modes are illustrated above.
The general solution is a sum over all possible values of 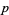 and
and 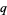 , so the final solution is
, so the final solution is
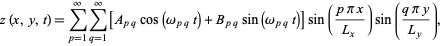 |
(17)
|
where 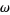 is defined by combining (◇) and (◇) to yield
is defined by combining (◇) and (◇) to yield
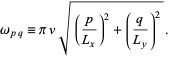 |
(18)
|
Given the initial conditions 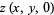 and
and 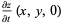 , we can compute the
, we can compute the 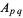 s and
s and 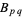 s explicitly. To accomplish this, we make use of the orthogonality of the sine function in the form
s explicitly. To accomplish this, we make use of the orthogonality of the sine function in the form
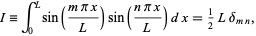 |
(19)
|
where 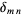 is the Kronecker delta. This can be demonstrated by direct integration. Let
is the Kronecker delta. This can be demonstrated by direct integration. Let 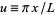 so
so 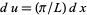 in (◇), then
in (◇), then
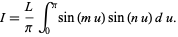 |
(20)
|
Now use the trigonometric identity
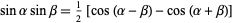 |
(21)
|
to write
![I=L/(2pi)int_0^picos[(m-n)u]du+int_0^picos[(m+n)u]du.](http://mathworld.wolfram.com/images/equations/WaveEquationRectangle/NumberedEquation22.gif) |
(22)
|
Note that for an integer 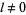 , the following integral vanishes
, the following integral vanishes
since 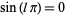 when
when 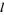 is an integer. Therefore,
is an integer. Therefore, 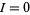 when
when 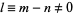 . However,
. However, 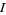 does not vanish when
does not vanish when 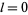 , since
, since
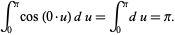 |
(27)
|
We therefore have that 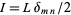 , so we have derived (◇). Now we multiply
, so we have derived (◇). Now we multiply 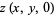 by two sine terms and integrate between 0 and
by two sine terms and integrate between 0 and 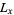 and between 0 and
and between 0 and 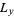 ,
,
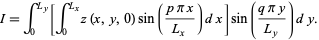 |
(28)
|
Now plug in 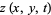 , set
, set 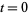 , and prime the indices to distinguish them from the
, and prime the indices to distinguish them from the 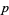 and
and 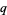 in (28),
in (28),
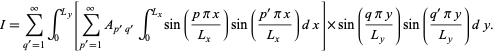 |
(29)
|
Making use of (◇) in (29),
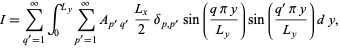 |
(30)
|
so the sums over 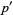 and
and 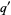 collapse to a single term
collapse to a single term
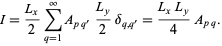 |
(31)
|
Equating (30) and (31) and solving for 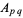 then gives
then gives
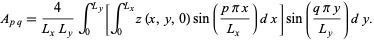 |
(32)
|
An analogous derivation gives the  s as
s as
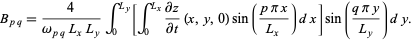 |
(33)
|
 الاكثر قراءة في المعادلات التفاضلية الجزئية
الاكثر قراءة في المعادلات التفاضلية الجزئية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


