

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Partial Differential Equation
المؤلف:
Arfken, G
المصدر:
"Partial Differential Equations of Theoretical Physics." §8.1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
الجزء والصفحة:
...
23-7-2018
4803
Partial Differential Equation
A partial differential equation (PDE) is an equation involving functions and their partial derivatives; for example, the wave equation
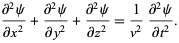 |
(1) |
Some partial differential equations can be solved exactly in the Wolfram Language using DSolve[eqn, y, {" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline1.gif" style="height:14px; width:5px" />x1, x2
}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline2.gif" style="height:14px; width:5px" />], and numerically using NDSolve[eqns, y,
{" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline3.gif" style="height:14px; width:5px" />x, xmin, xmax
}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline4.gif" style="height:14px; width:5px" />,
{" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline5.gif" style="height:14px; width:5px" />t, tmin, tmax
}" src="http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/Inline6.gif" style="height:14px; width:5px" />].
In general, partial differential equations are much more difficult to solve analytically than are ordinary differential equations. They may sometimes be solved using a Bäcklund transformation, characteristics, Green's function, integral transform, Lax pair, separation of variables, or--when all else fails (which it frequently does)--numerical methods such as finite differences.
Fortunately, partial differential equations of second-order are often amenable to analytical solution. Such PDEs are of the form
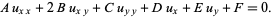 |
(2) |
Linear second-order PDEs are then classified according to the properties of the matrix
![Z=[A B; B C]](http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/NumberedEquation3.gif) |
(3) |
as elliptic, hyperbolic, or parabolic.
If 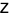 is a positive definite matrix, i.e.,
is a positive definite matrix, i.e., 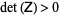 , the PDE is said to be elliptic. Laplace's equation and Poisson's equation are examples. Boundary conditions are used to give the constraint
, the PDE is said to be elliptic. Laplace's equation and Poisson's equation are examples. Boundary conditions are used to give the constraint 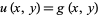 on
on 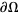 , where
, where
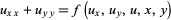 |
(4) |
holds in 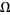 .
.
If det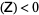 , the PDE is said to be hyperbolic. The wave equation is an example of a hyperbolic partial differential equation. Initial-boundary conditions are used to give
, the PDE is said to be hyperbolic. The wave equation is an example of a hyperbolic partial differential equation. Initial-boundary conditions are used to give
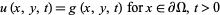 |
(5) |
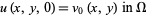 |
(6) |
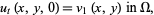 |
(7) |
where
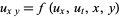 |
(8) |
holds in 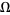 .
.
If det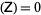 , the PDE is said to be parabolic. The heat conduction equation equation and other diffusion equations are examples. Initial-boundary conditions are used to give
, the PDE is said to be parabolic. The heat conduction equation equation and other diffusion equations are examples. Initial-boundary conditions are used to give
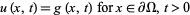 |
(9) |
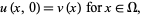 |
(10) |
where
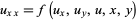 |
(11) |
holds in 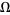 .
.
The following are examples of important partial differential equations that commonly arise in problems of mathematical physics.
Benjamin-Bona-Mahony equation
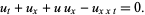 |
(12) |
Biharmonic equation
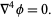 |
(13) |
Boussinesq equation
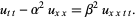 |
(14) |
Cauchy-Riemann equations
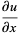 |
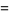 |
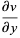 |
(15) |
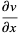 |
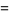 |
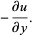 |
(16) |
Chaplygin's equation
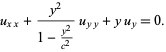 |
(17) |
Euler-Darboux equation
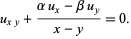 |
(18) |
Heat conduction equation
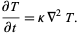 |
(19) |
Helmholtz differential equation
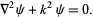 |
(20) |
Klein-Gordon equation
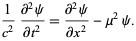 |
(21) |
Korteweg-de Vries-Burgers equation
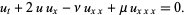 |
(22) |
Korteweg-de Vries equation
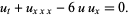 |
(23) |
Krichever-Novikov equation
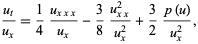 |
(24) |
where
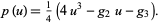 |
(25) |
Laplace's equation
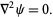 |
(26) |
Lin-Tsien equation
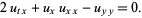 |
(27) |
Sine-Gordon equation
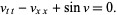 |
(28) |
Spherical harmonic differential equation
![[1/(sintheta)partial/(partialtheta)(sinthetapartial/(partialtheta))+1/(sin^2theta)(partial^2)/(partialphi^2)+l(l+1)]u=0.](http://mathworld.wolfram.com/images/equations/PartialDifferentialEquation/NumberedEquation27.gif) |
(29) |
Tricomi equation
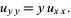 |
(30) |
Wave equation
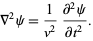 |
(31) |
REFERENCES:
Arfken, G. "Partial Differential Equations of Theoretical Physics." §8.1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 437-440, 1985.
Bateman, H. Partial Differential Equations of Mathematical Physics. New York: Dover, 1944.
Conte, R. "Exact Solutions of Nonlinear Partial Differential Equations by Singularity Analysis." 13 Sep 2000. http://arxiv.org/abs/nlin.SI/0009024.
Kamke, E. Differentialgleichungen Lösungsmethoden und Lösungen, Bd. 2: Partielle Differentialgleichungen ester Ordnung für eine gesuchte Function. New York: Chelsea, 1974.
Folland, G. B. Introduction to Partial Differential Equations, 2nd ed. Princeton, NJ: Princeton University Press, 1996.
Kevorkian, J. Partial Differential Equations: Analytical Solution Techniques, 2nd ed. New York: Springer-Verlag, 2000.
Morse, P. M. and Feshbach, H. "Standard Forms for Some of the Partial Differential Equations of Theoretical Physics." Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 271-272, 1953.
Polyanin, A.; Zaitsev, V.; and Moussiaux, A. Handbook of First-Order Partial Differential Equations. New York: Gordon and Breach, 2001.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Partial Differential Equations." Ch. 19 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 818-880, 1992.
Sobolev, S. L. Partial Differential Equations of Mathematical Physics. New York: Dover, 1989.
Sommerfeld, A. Partial Differential Equations in Physics. New York: Academic Press, 1964.
Taylor, M. E. Partial Differential Equations, Vol. 1: Basic Theory. New York: Springer-Verlag, 1996.
Taylor, M. E. Partial Differential Equations, Vol. 2: Qualitative Studies of Linear Equations. New York: Springer-Verlag, 1996.
Taylor, M. E. Partial Differential Equations, Vol. 3: Nonlinear Equations. New York: Springer-Verlag, 1996.
Trott, M. "The Mathematica Guidebooks Additional Material: Various Time-Dependent PDEs." http://www.mathematicaguidebooks.org/additions.shtml#N_1_06.
Webster, A. G. Partial Differential Equations of Mathematical Physics, 2nd corr. ed. New York: Dover, 1955.
Weisstein, E. W. "Books about Partial Differential Equations." http://www.ericweisstein.com/encyclopedias/books/PartialDifferentialEquations.html.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.
 الاكثر قراءة في المعادلات التفاضلية الجزئية
الاكثر قراءة في المعادلات التفاضلية الجزئية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















