Heat Conduction Equation--Disk
المؤلف:
Bowman, F
المصدر:
Introduction to Bessel Functions. New York: Dover, 1958.
الجزء والصفحة:
...
13-7-2018
1513
Heat Conduction Equation--Disk
To solve the heat conduction equation on a two-dimensional disk of radius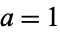 
, try to separate the equation using
 |
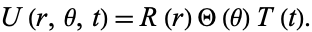(1)
|
Writing the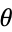 
and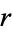 
terms of the Laplacian in cylindrical coordinates gives
 |
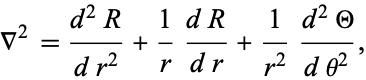(2)
|
so the heat conduction equation becomes
 |
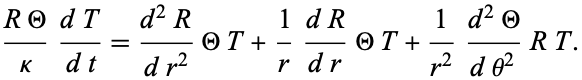(3)
|
Multiplying through by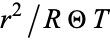 
gives
 |
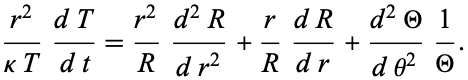(4)
|
The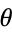 
term can be separated.
 |
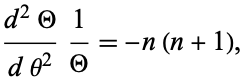(5)
|
which has a solution
![Theta(theta)=Acos[sqrt(n(n+1))theta]+Bsin[sqrt(n(n+1))theta].](http://mathworld.wolfram.com/images/equations/HeatConductionEquationDisk/NumberedEquation6.gif) |
(6)
|
The remaining portion becomes
 |
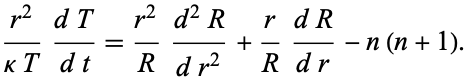(7)
|
Dividing by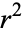 
gives
 |
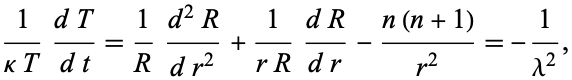(8)
|
where a negative separation constant has been chosen so that the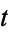 
portion remains finite
 |
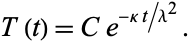(9)
|
The radial portion then becomes
 |
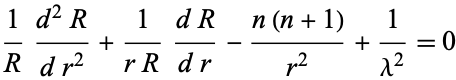(10)
|
![r^2(d^2R)/(dr^2)+r(dR)/(dr)+[(r^2)/(lambda^2)-n(n+1)]R=0,](http://mathworld.wolfram.com/images/equations/HeatConductionEquationDisk/NumberedEquation11.gif) |
(11)
|
which is the spherical Bessel differential equation.
Consider disk or radius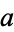 
with initial temperature 
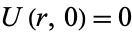and the boundary condition 
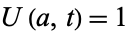. Then the solution is
 |
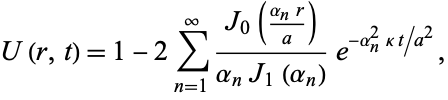(12)
|
where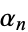 
is the 
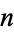th positive zero of the Bessel function of the first kind 
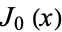(Bowman 1958, pp. 37-39).
REFERENCES:
Bowman, F. Introduction to Bessel Functions. New York: Dover, 1958.
Carslaw, H. S. and Jaeger, J. C. "Some Two-Dimensional Problems in Conduction of Heat with Circular Symmetry." Proc. London Math. Soc. 46, 361-388, 1940.
الاكثر قراءة في المعادلات التفاضلية الجزئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
