

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Heat Conduction Equation
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
المرجع الالكتروني للمعلوماتيه
الجزء والصفحة:
...
13-7-2018
2100
Heat Conduction Equation
A partial differential diffusion equation of the form
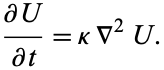 |
(1) |
Physically, the equation commonly arises in situations where 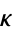 is the thermal diffusivity and
is the thermal diffusivity and 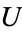 the temperature.
the temperature.
The one-dimensional heat conduction equation is
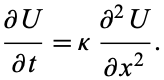 |
(2) |
This can be solved by separation of variables using
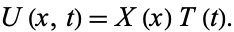 |
(3) |
Then
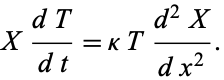 |
(4) |
Dividing both sides by 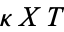 gives
gives
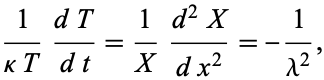 |
(5) |
where each side must be equal to a constant. Anticipating the exponential solution in 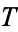 , we have picked a negative separation constant so that the solution remains finite at all times and
, we have picked a negative separation constant so that the solution remains finite at all times and 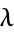 has units of length. The
has units of length. The 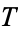 solution is
solution is
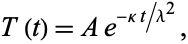 |
(6) |
and the 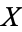 solution is
solution is
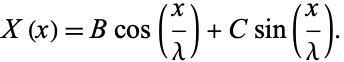 |
(7) |
The general solution is then
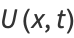 |
 |
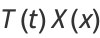 |
(8) |
 |
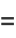 |
![Ae^(-kappat/lambda^2)[Bcos(x/lambda)+Csin(x/lambda)]](http://mathworld.wolfram.com/images/equations/HeatConductionEquation/Inline13.gif) |
(9) |
 |
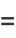 |
![e^(-kappat/lambda^2)[Dcos(x/lambda)+Esin(x/lambda)].](http://mathworld.wolfram.com/images/equations/HeatConductionEquation/Inline16.gif) |
(10) |
If we are given the boundary conditions
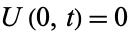 |
(11) |
and
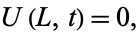 |
(12) |
then applying (11) to (10) gives
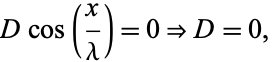 |
(13) |
and applying (12) to (10) gives
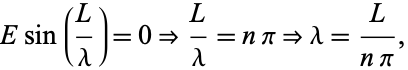 |
(14) |
so (10) becomes
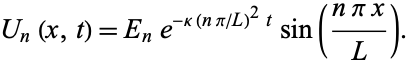 |
(15) |
Since the general solution can have any 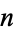 ,
,
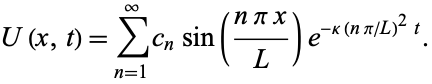 |
(16) |
Now, if we are given an initial condition 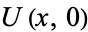 , we have
, we have
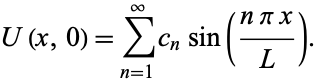 |
(17) |
Multiplying both sides by 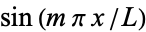 and integrating from 0 to
and integrating from 0 to 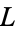 gives
gives
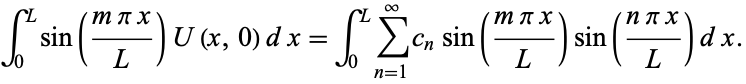 |
(18) |
Using the orthogonality of 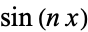 and
and 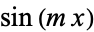 ,
,
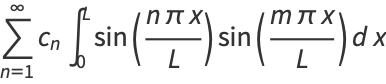 |
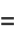 |
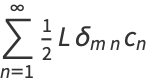 |
(19) |
 |
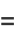 |
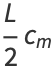 |
(20) |
 |
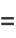 |
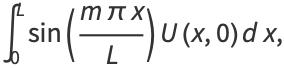 |
(21) |
so
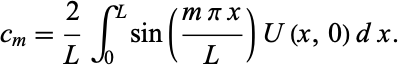 |
(22) |
If the boundary conditions are replaced by the requirement that the derivative of the temperature be zero at the edges, then (◇) and (◇) are replaced by
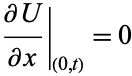 |
(23) |
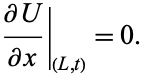 |
(24) |
Following the same procedure as before, a similar answer is found, but with sine replaced by cosine:
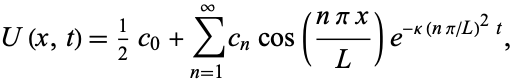 |
(25) |
where
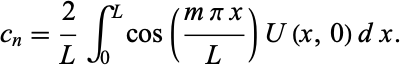 |
(26) |
 الاكثر قراءة في المعادلات التفاضلية الجزئية
الاكثر قراءة في المعادلات التفاضلية الجزئية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















