Alternating current (AC) circuits are made up of e.m.f. sources and three different types of passive element; resistors, inductors, and capacitors, Resistors satisfy Ohm's law:

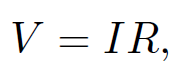 (1.1)

where R is the resistance, I is the current flowing through the resistor, and V is the voltage drop across the resistor (in the direction in which the current flows). Inductors satisfy

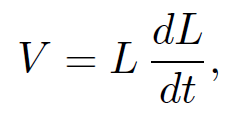 (1.2)

where L is the inductance. Finally, capacitors obey

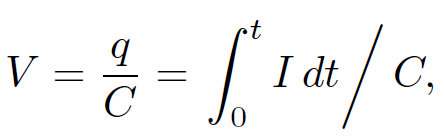 (1.3)

where C is the capacitance, q is the charge stored on the plate with the more positive potential, and I = 0 for t < 0. Note that any passive component of a real electrical circuit can always be represented as a combination of ideal resistors, inductors, and capacitors. Let us consider the classic LCR circuit, which consists of an inductor L, a capacitor C, and a resistor R, all connected in series with an e.m.f. source V . The circuit equation is obtained by setting the input voltage V equal to the sum of the voltage drops across the three passive elements in the circuit. Thus,

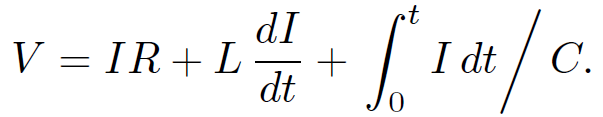 (1.4)

This is an integro-differential equation which, in general, is quite tricky to solve. Suppose, however, that both the voltage and the current oscillate at some angular frequency 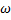, so that

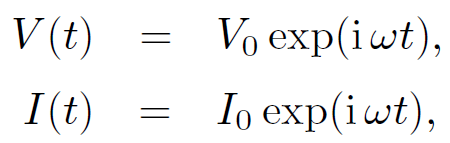 (1.5)

where the physical solution is understood to be the real part of the above expressions. The assumed behaviour of the voltage and current is clearly relevant to electrical circuits powered by the mains voltage (which oscillates at 60 hertz). Equations (1.4) and (1.5) yield

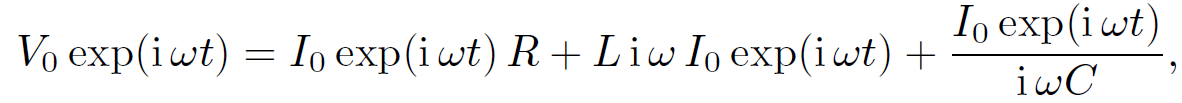 (1.6)

giving

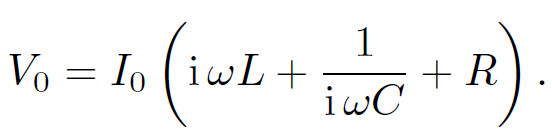 (1.7)

It is helpful to define the ''impedance" of the circuit;

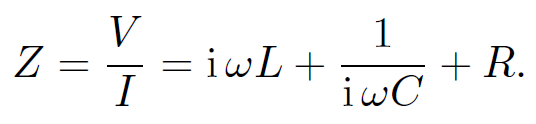 (1.8)

Impedance is a generalization of the concept of resistance. In general, the impedance of an AC circuit is a complex quantity. The average power output of the e.m.f. source is

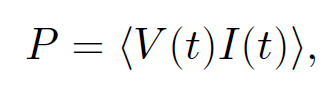 (1.9)

where the average is taken over one period of the oscillation. Let us, first of all, calculate the power using real (rather than complex) voltages and currents. We can write

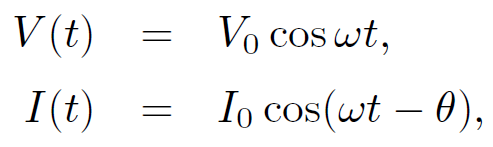 (1.10)

where θ is the phase lag of the current with respect to the voltage. It follows that

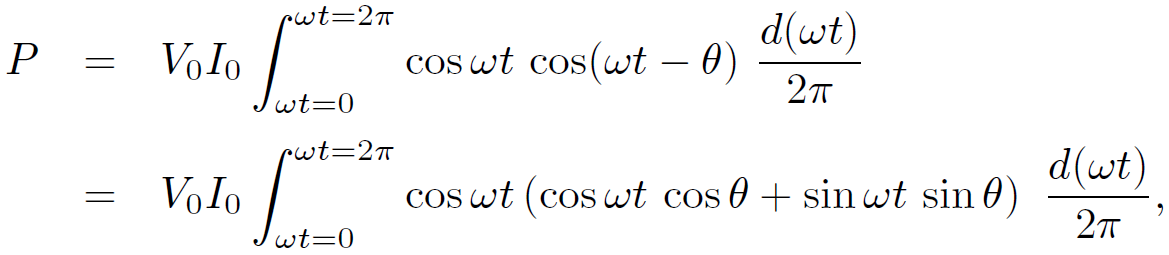 (1.11)

giving

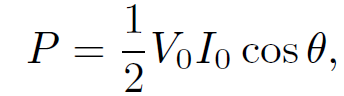 (1.12)

since 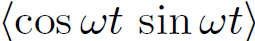 = 0 and 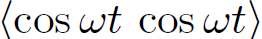= 1/2. In complex representation, the voltage and the current are written

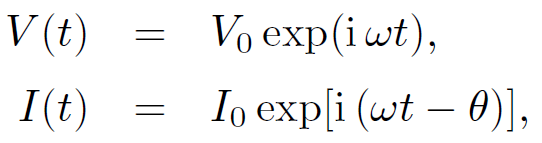 (1.13)

where I₀ and V₀ are assumed to be real quantities. Note that

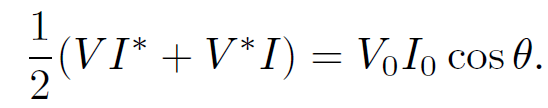 (1.14)

It follows that

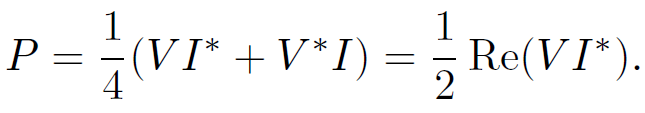 (1.15)

Making use of Eq. (1.8), we find that

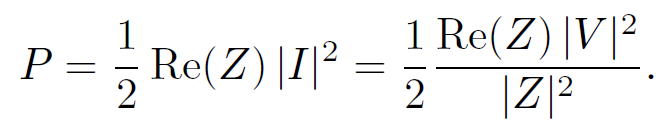 (1.16)

Note that power dissipation is associated with the real part of the impedance. For the special case of an LCR circuit,

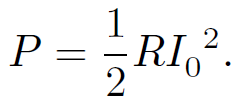 (1.17)

It is clear that only the resistor dissipates energy in this circuit. The inductor and the capacitor both store energy, but they eventually return it to the circuit without dissipation. According to Eq. (1.8), the amplitude of the current which flows in an LCR circuit for a given amplitude of the input voltage is given by

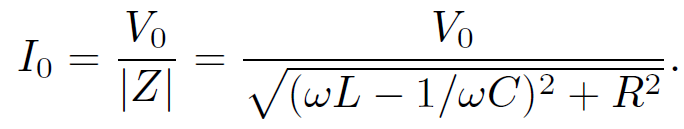 (1.18)

The response of the circuit is clearly resonant, peaking at 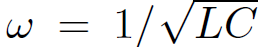, and preaching 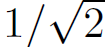of the peak value at  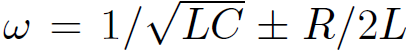(assuming that R << 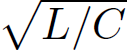). In fact, LCR circuits are used in radio tuners to filter out signals whose frequencies fall outside a given band. The phase lag of the current with respect to the voltage is given by

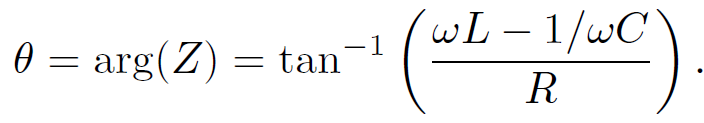 (1.19)

The phase lag varies from –π/2 for frequencies significantly below the resonant frequency, to zero at the resonant frequency(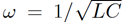), to π/2 for frequencies significantly above the resonant frequency. It is clear that in conventional AC circuits the circuit equation reduces to a simple algebraic equation, and the behaviour of the circuit is summed up by the impedance Z. The real part of Z tells us the power dissipated in the circuit, the magnitude of Z gives the ratio of the peak current to the peak voltage, and the argument of Z gives the phase lag of the current with respect to the voltage.

مواضيع ذات صلة

Thermal conductivity

Molecular diffusion

Ionic conductivity

The drift speed

Electrical transients

الشرر المقدس

الحقول الكهربية والشرر

الخلق غير المرئي

عجائب الكهرباء

مصادر الطاقة الكهربائية

التيارات الكهربائية التي تجري إلى الابد

النقل الكهربائي وقانون أوم