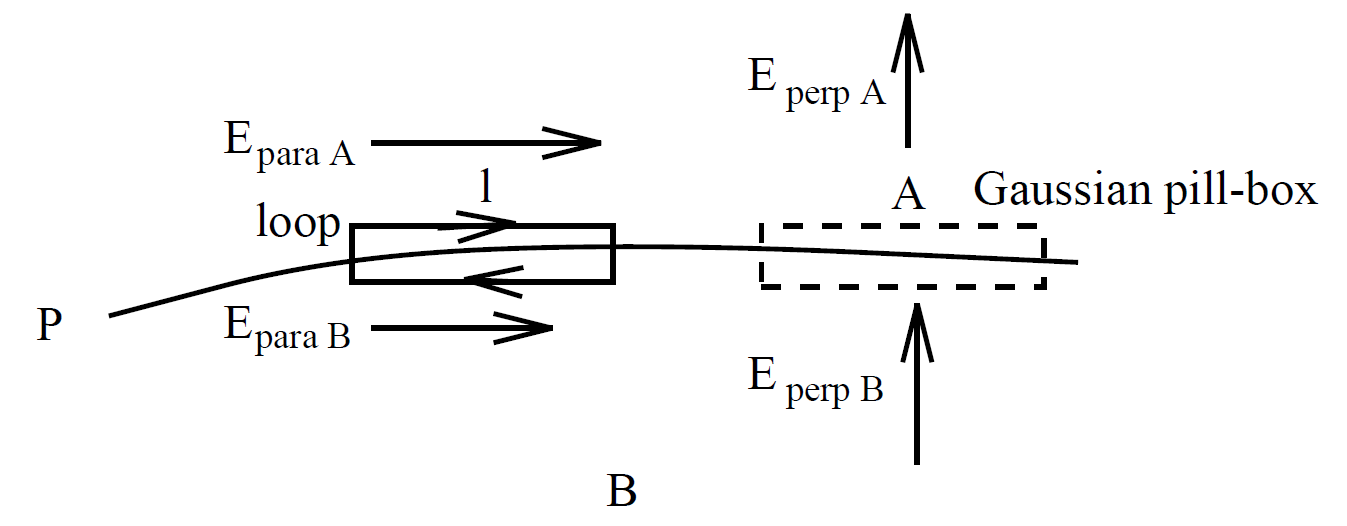
What are the most general boundary conditions satisfied by the electric field at the interface between two mediums; e.g., the interface between a vacuum and a conductor? Consider an interface P between two mediums A and B. Let us, first

of all, integrate Gauss' law,

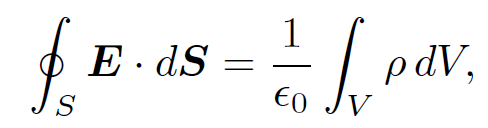 (1.1)

over a Gaussian pill-box S of cross-sectional area A whose two ends are locally parallel to the interface. The ends of the box can be made arbitrarily close together. In this limit, the flux of the electric field out of the sides of the box is obviously negligible. The only contribution to the flux comes from the two ends. In fact

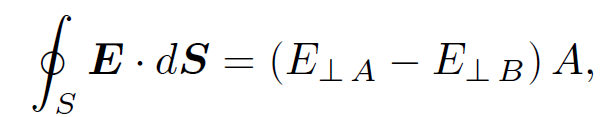 (1.2)

where E_┴A is the perpendicular (to the interface) electric field in medium A at the interface, etc. The charge enclosed by the pill-box is simply σ A, where σ is the sheet charge density on the interface. Note that any volume distribution of charge gives rise to a negligible contribution to the right-hand side of the above equation in the limit where the two ends of the pill-box are very closely spaced. Thus, Gauss' law yields

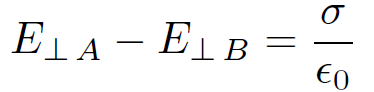 (1.3)

at the interface; i.e., the presence of a charge sheet on an interface causes a discontinuity in the perpendicular component of the electric field. What about the parallel electric field? Let us integrate Faraday's law,

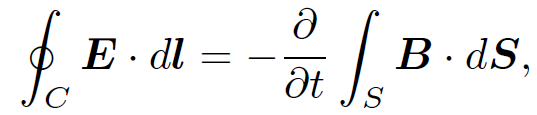 (1.4)

around a rectangular loop C whose long sides, length l, run parallel to the interface. The length of the short sides is assumed to be arbitrarily small. The dominant contribution to the loop integral comes from the long sides:

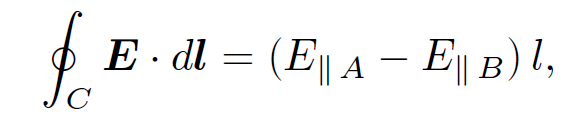 (1.5)

where E_║A is the parallel (to the interface) electric field in medium A at the interface, etc. The flux of the magnetic field through the loop is approximately B_┴ A, where B_┴ is the component of the magnetic field which is normal to the loop, and A is the area of the loop. But, A → 0 as the short sides of the loop are shrunk to zero so, unless the magnetic field becomes infinite (we assume that it does not), the flux also tends to zero. Thus,

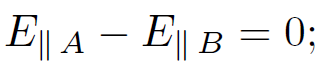 (1.6)

i.e., there can be no discontinuity in the parallel component of the electric field across an interface.

مواضيع ذات صلة

Thermal conductivity

Molecular diffusion

Ionic conductivity

The drift speed

Electrical transients

الشرر المقدس

الحقول الكهربية والشرر

الخلق غير المرئي

عجائب الكهرباء

مصادر الطاقة الكهربائية

التيارات الكهربائية التي تجري إلى الابد

النقل الكهربائي وقانون أوم