الجمع المثلثي للمتجهات

سيكون من السهل عليك جمع الإزاحات لنفرض مثلاً ان جشرة على سطح منضدة وتقوم بالإزاحات المبينة بالشكل1)).

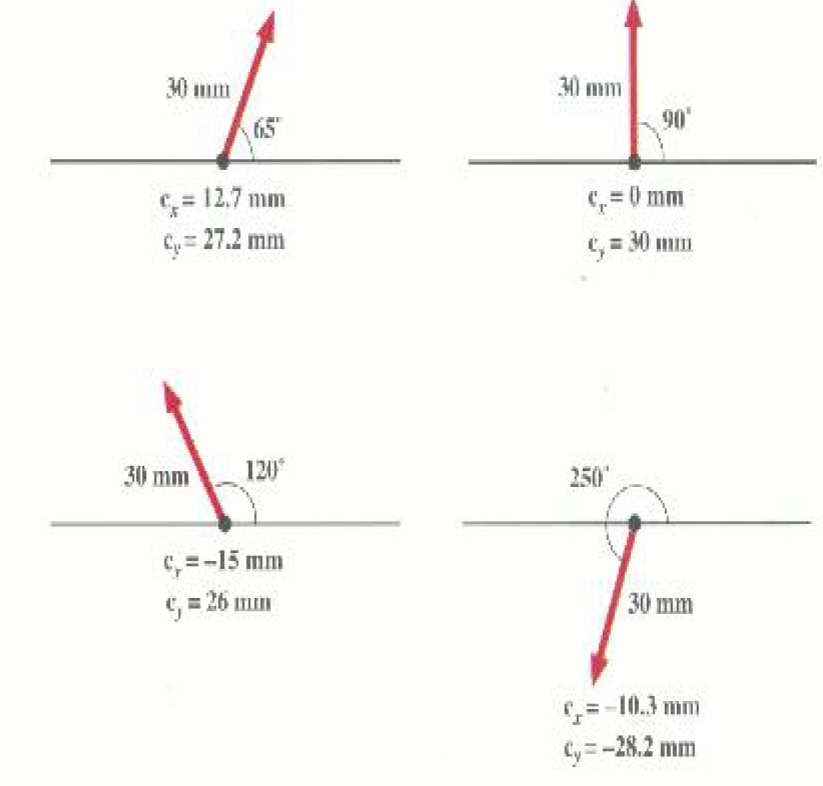
 (1)

30.0 mm بزاوية 65.0 ^o بالنسبة للاتجاه الموجب للمحور x (الشرق).

30.0 mm بزاوية 90.0^o

30.0 mm بزاوية 120.0^o

30.0 mm بزاوية 250.0^o

من الممكن بالطبع إيجاد المحصلة بيانياً باستخدام رسم بياني المتجهات المبين بالشكل 2))، ولكن هذه الطريقة تصبح مرهقة تماماً في هذه الحالة. الطريقة الأسهل

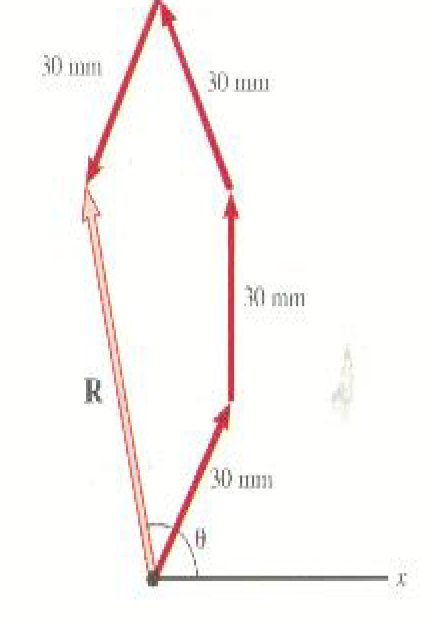
( (2

هي أن نستخدم مركبتي كل من هذه المتجهات لإيجاد مركبتي المحصلة. وللحصول على المركبة x: ولتكن R_x ، علينا ببساطة أن نجمع المركبات x للمتجهات الأصلية والسابق إيجادها في الشكل ((1:

R_x= 12.7 + 0 + (-15.0) + (-10.3)mm 

12.7 + 0 - 15.0 - 10.3 = -12.6 mm=

وبالمثل يمكن إيجاد المركبة y للمحصلة R_y بجمع المركبات y للمتجهات الأصلية :

R_y= 27.2 + 30.0 + 26.0 - 28.2 =55.0 mm 

هاتان هما المركبتان المتعامدتان للمحصلة. لاحظ أن R_x سالبة ولذلك فهي في الاتجاه السالب للمحور x. من الضروري إذن ان تؤخذ إشارات المركبات في الاعتبار عند تعيين  المجموع. لاحظ أيضاً انك تستطيع جمع المركبات بأي ترتيب تراه ، كما في الجمع البياني ، لأن هذا لن يغير النتيجة.

يمثل الشكل 3)) المحصلة R ومركبتيها المتعامدتين. ذلك أن المحصلة هي وتر مثلث قائم الزاوية ضلعاه الآخران هما R_x = 12.6 mm و R_y = 55.0 mm. وباستخدام نظرية فيثاغورس سنجد ان مقدار R هو

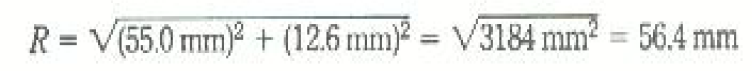
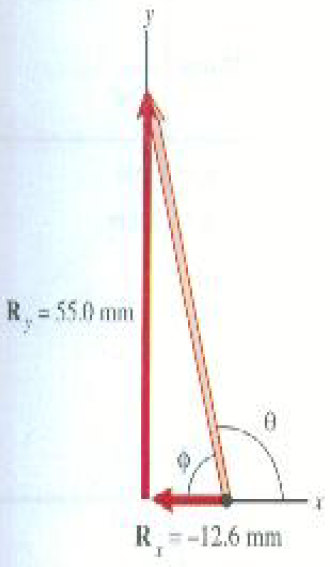
(3)

ولإيجاد الزاوية θ التي صنعها المحصلة مع المحور x علينا أولاً إيجاد الزاوية θ في الشكل3) ). لاحظ ان:

علينا الآن إيجاد الزاوية Ø التي ظلها 4.37. هذه الزاوية تسمى معكوس الظل وتكتب على الصور inv tan  أو tan^-1 . وباستعمال الجداول المثلثية أو الآلة الحاسبة اليدوية ستجد أن

 tan^-1 (4.37^o) = 77.0^o= Ø

وحيث ان 180^o = Ø + θ إذن

=103^o Ø        =180^oθ

مواضيع ذات صلة

القاعدة الأساسية لدفع الصاروخ

ثورة هايزنبرج: من يقين العلم إلى مسؤولية العلماء

الفزياء والكون .. تجربة ميكسلون ومورلي

الضوء

البلازما والفضاء

الكون المتحرك

الفيزياء والكون .. البلازما

الفيزياء والكون.. الذرة

قانون التوازن في كون الله الواسع

الفيزياء والكون جزيء الفا

وصف معجل «البيليترون »

دور الجدران المادية في حصر المادة البلازمية