

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
The Handshake Problem
المؤلف:
W.D. Wallis
المصدر:
Mathematics in the Real World
الجزء والصفحة:
124-125
12-2-2016
1883
We conclude with an old puzzle that can be solved using a graph representation.
Eight people—four married couples—attend a dinner party. Various introductions are made; everybody shakes hands (once!) with some of the others. Of course, no one shakes hands with his/her spouse.
After a while, the hostess asks every other person in the room, “how many times did you shake hands tonight?” It turns out that no two of the people she asked said that they shook hands the same number of times. (The hostess isn’t included of course; she didn’t ask herself.)
How many times had the host (the hostess’ spouse) shaken hands?
We use graph theory to represent the elements of the problem. Write W,X,Y,Z, w,x,y,z for the eight people; W and w are one couple, X and x another, and so on.
We represent the party by a graph with people as vertices and handshakes as edges.
The number of handshakes is the degree of the vertex.
No one shook hands with more than six others (there are only six other people other than the two members of any couple). So the numbers of times people (other than the hostess) shook hands are seven different whole numbers, ranging from 0 to 6. It follows that each of 0, 1, 2, 3, 4, 5, 6 occurs exactly once among the degrees of those other than the hostess.
So somebody shook hands six times.
Let’s call this person X. He or she did not shake hands with his/her spouse x, so he/she shook with everybody else. These handshakes contribute the edges shown in the figure shown right:
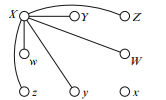
Somebody shook hands 0 times. Looking at the figure, every vertex received at least one edge, except for x. (There might be further edges, not yet shown.) So x must be the person with no edges (no handshakes). No matter what happens, you will never add an edge touching x.
Now, somebody shook hands exactly five times. It was neither X nor x. Suppose it was Y. There is already one edge touching Y, the edge XY, so there are exactly four more edges touching Y. None of the new edges touch x or y (remember, people don’t shake with spouses). This implies that y is the only person to receive exactly only one: x has 0, and every other vertex has at least 2. The figure looks like the following (possibly with more edges):
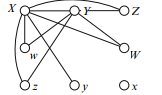
Next, someone shook hands exactly four times. It cannot be X, x, Y or y; say it is Z. There are already two edges touching Z, and Z is not joined to z. So Z must be joined to W and w. We have obtained the following graph, showing all the handshakes:
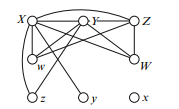
In this graph there are two vertices of degree 3 (W and w), and each of 0,1,2,3,4,5 occurs as a degree once. One of the two vertices of degree 3 must be the hostess (this is the only possible way to get a repeat), and the other is her spouse. So the host shook hands three times.