Consider these two diagrams.

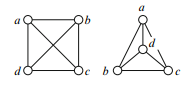
They represent the same graph, the complete graph K4 on four vertices. But as diagrams they are quite different: in the left-hand version, two edges cross; in theright-hand diagram there are no crossings. We shall refer to the two diagrams as different representations of K₄. The crossing number of a representation is the number of different pairs of edges that cross. A graph that can be drawn without any crossings is called planar and a drawing of a graph with no crossings is called a planar representation. For example, K₄ is planar and the right-hand drawing is a planar representation of K₄.

Sample Problem 1.1 Show that the crossing number of the complete graph K₅on five vertices is 1.

Solution. We can think of K5 as being K4 with one more vertex added. If we start with the representation shown in the left-hand of the diagram, we certainly get at least one crossing, and it is not hard to avoid further crossings. So the crossing number of K5 is either 0 or 1. To obtain a planar representation of K₅ we would have to add a new vertex, e say, to the right-hand diagram. But if the new vertex is inside the old diagram, at least one new crossing will be introduced— for example, if it is inside the triangle bcd, edge ae must cross one of the original edges—and if e is outside the original diagram, de must cross another edge. The following diagrams illustrate these two cases.

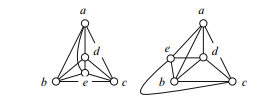
So K₅ has crossing number 1.

It is easy to see that any tree has crossing number 0. Similarly, any cycle can be drawn without crossings.

مواضيع ذات صلة

Minimum Spanning Tree

Maximum Leaf Number

Lobster Graph

Labeled Tree

Internal Path Length

Red-Black Tree

Pseudotree

Pseudoforest

Prüfer Code

Planted Tree

Planted Planar Tree

Graph Strength