We shall define a spanning subgraph of a graph G to be a subgraph that contains every vertex of G. A spanning tree in a graph is a spanning subgraph that is a tree when considered as a graph in its own right.

It is easy to show that any connected graph G has a spanning tree. If G is a tree,  then the whole of G is itself the spanning tree. Otherwise G must contain a cycle;  delete one edge from the cycle. The resulting graph is still a connected subgraph of G; and, as no vertex has been deleted, it is a spanning subgraph. Find a cycle in this new graph and delete it; repeat the process. Eventually the remaining graph will contain no cycle, so it is a tree. So when the process stops, we have found a spanning tree.

A given graph might have many different spanning trees. There are algorithms to find all spanning trees in a graph. But fortunately a complete search for spanning trees can be done quite quickly in a small graph. We’ll look at an example.

Sample Problem 1.1 Find all spanning trees in the following graph.

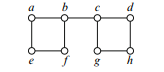
Solution. The graph contains two cycles, ab f e and cdhg. In order to construct a tree, it is necessary to delete at least one edge from each of these cycles. As the original graph contains eight vertices, any spanning tree will have eight vertices.

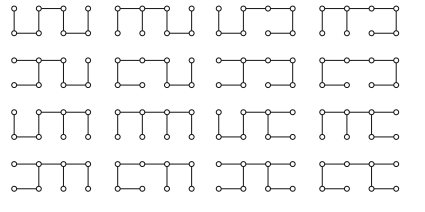
From Theorem 1in(Trees), these trees will have seven edges. So exactly one edge must be removed from each cycle, or there will be too few edges. (This argument would need some modification if an edge that was common to both cycles were deleted,  but fortunately the graph contains no such edge.) So there are 16 spanning trees,  as follows:

مواضيع ذات صلة

Minimum Spanning Tree

Maximum Leaf Number

Lobster Graph

Labeled Tree

Internal Path Length

Red-Black Tree

Pseudotree

Pseudoforest

Prüfer Code

Planted Tree

Planted Planar Tree

Graph Strength