
العدسات في مجموعات متلاصقة
 المؤلف:
فريدريك بوش ، دافيد جيرد
المؤلف:
فريدريك بوش ، دافيد جيرد
 المصدر:
اساسيات الفيزياء
المصدر:
اساسيات الفيزياء
 الجزء والصفحة:
الجزء والصفحة:
 10-1-2016
10-1-2016
 3163
3163
العدسات في مجموعات متلاصقة
قد تكون ممن فحصوا نظرهم ولاحظت أن الطبيب يضع أحياناً أكثر من عدسة معاً أمام عينك. ولكي يصل الطبيب إلى أفضل مجموعة من العدسات فلا بد له من وسيلة يجمع بها تأثير العدسات الرقيقة المتلاصقة. ومن السهل اشتقاق الصيغة الضرورية البسيطة.
ويعطي موقع الصورة المتكونة بواسطة العدسة الأولى من المعادلة:
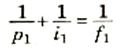
سنفحص الآن الحالة التي تكون فيها العدسة رقم 1 مجمعة وتكون صورة حقيقية وبما أن هذه الصورة ستقع خلف العدسة رقم 1 فلا بد أن تكون أيضاً خلف العدسة رقم 2 لأننا سنعتبر العدستين عند نفس الموقع عملياً، وهذا هو ما عنيناه بقولنا أن المسافة بين العدسات مهملة إلى جانب أبعادها البؤرية. وهكذا تكون الصورة الأولى جسماً تقديرياً للعدسة 2 ولذا فإن p2 = -i1 طبقاً لقاعدة الإشارات وتعطينا معادلة العدسة 2 ما يلي:

وبجمع معادلتي معاً فإن i1 تختفي:
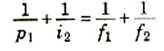
وكما يتضح من الشكل 1))، فإن p1 هو موقع الجسم الأصلي i2 هو موقع الصورة النهائية. أي ان هذه المعادلة هي نفس معادلة العدسة بالنسبة لعدسة منفردة بعدها البؤري f يعطي بالعلاقة:
(1) 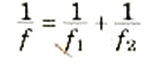
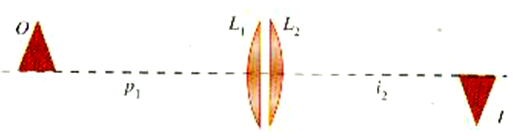
الشكل 1)): عندما تكون العدستان متلاصقتين معاً فإن تأثيرهما المزدوج هو أنهما تعملان كعدسة منفردة بعدها البؤري هو: 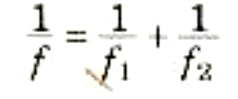
ويمكن مد استعمال المعادلة (1) لتشمل أكثر من عدستين وكلها متلاصقة طالما كان سمك المجموعة مهملاً إذا قرون بالأبعاد البؤرية المنفردة. كما أن هذه المعادلة تنطبق أيضاً على أية مجموعة من العدسات المجمعة والمفرقة طالما استعملت الإشارات الصحيحة للأبعاد البؤرية.
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


