Equation (44.7) or (44.12) can be interpreted in a special way.

Working always with reversible engines, a heat Q₁ at temperature T₁ is “equivalent” to Q₂ at T₂ if Q₁/T₁=Q₂/T₂, in the sense that as one is absorbed the other is delivered. This suggests that if we call Q/T something, we can say: in a reversible process as much Q/T is absorbed as is liberated; there is no gain or loss of Q/T. This Q/T is called entropy, and we say “there is no net change in entropy in a reversible cycle.” If T is 1^∘, then the entropy is QS/1^∘ or, as we symbolized it, QS/1^∘=S. Actually, S is the letter usually used for entropy, and it is numerically equal to the heat (which we have called QS) delivered to a 1^∘-reservoir (entropy is not itself a heat, it is heat divided by a temperature, hence it is measured in joules per degree).

Now it is interesting that besides the pressure, which is a function of the temperature and the volume, and the internal energy, which is a function of temperature and volume, we have found another quantity which is a function of the condition, i.e., the entropy of the substance. Let us try to explain how we compute it, and what we mean when we call it a “function of the condition.” Consider the system in two different conditions, much as we had in the experiment where we did the adiabatic and isothermal expansions. (Incidentally, there is no need that a heat engine have only two reservoirs, it could have three or four different temperatures at which it takes in and delivers heats, and so on.) We can move around on a pV diagram all over the place, and go from one condition to another. In other words, we could say the gas is in a certain condition a, and then it goes over to some other condition, b, and we will require that this transition, made from a to b, be reversible. Now suppose that all along the path from a to b we have little reservoirs at different temperatures, so that the heat dQ removed from the substance at each little step is delivered to each reservoir at the temperature corresponding to that point on the path. Then let us connect all these reservoirs, by reversible heat engines, to a single reservoir at the unit temperature. When we are finished carrying the substance from a to b, we shall bring all the reservoirs back to their original condition. Any heat dQ that has been absorbed from the substance at temperature T has now been converted by a reversible machine, and a certain amount of entropy dS has been delivered at the unit temperature as follows:

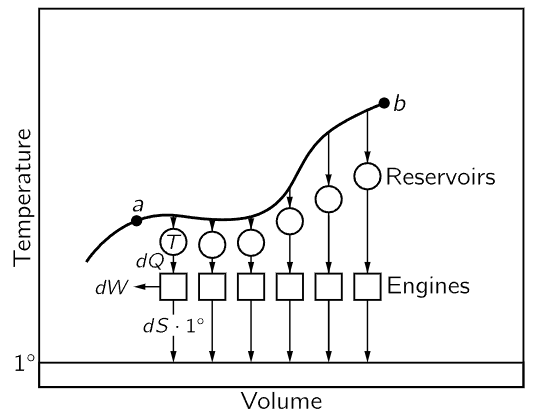
Fig. 44–10. Change in entropy during a reversible transformation.

Let us compute the total amount of entropy which has been delivered. The entropy difference, or the entropy needed to go from a to b by this particular reversible transformation, is the total entropy, the total of the entropy taken out of the little reservoirs, and delivered at the unit temperature:

The question is, does the entropy difference depend upon the path taken? There is more than one way to go from a to b. Remember that in the Carnot cycle we could go from a to c in Fig. 44–6 by first expanding isothermally and then adiabatically; or we could first expand adiabatically and then isothermally. So the question is whether the entropy change which occurs when we go from a to b in Fig. 44–10 is the same on one route as it is on another. It must be the same, because if we went all the way around the cycle, going forward on one path and backward on another, we would have a reversible engine, and there would be no loss of heat to the reservoir at unit temperature. In a totally reversible cycle, no heat must be taken from the reservoir at the unit temperature, so the entropy needed to go from a to b is the same over one path as it is over another. It is independent of path, and depends only on the endpoints. We can, therefore, say that there is a certain function, which we call the entropy of the substance, that depends only on the condition, i.e., only on the volume and temperature.

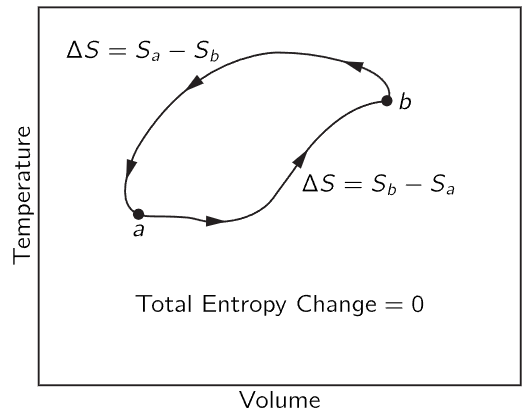
Fig. 44–11. Change in entropy in a completely reversible cycle.

We can find a function S(V,T) which has the property that if we compute the change in entropy, as the substance is moved along any reversible path, in terms of the heat rejected at unit temperature, then

where dQ is the heat removed from the substance at temperature T. This total entropy change is the difference between the entropy calculated at the initial and final points:

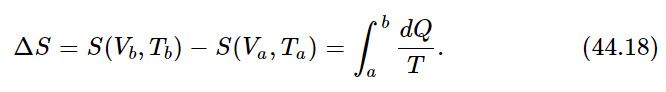
This expression does not completely define the entropy, but rather only the difference of entropy between two different conditions. Only if we can evaluate the entropy for one special condition can we really define S absolutely.

For a long time it was believed that absolute entropy meant nothing—that only differences could be defined—but finally Nernst proposed what he called the heat theorem, which is also called the third law of thermodynamics. It is very simple. We will say what it is, but we will not explain why it is true. Nernst’s postulate states simply that the entropy of any object at absolute zero is zero. We know of one case of T and V, namely T=0, where S is zero; and so we can get the entropy at any other point.

To give an illustration of these ideas, let us calculate the entropy of a perfect gas. In an isothermal (and therefore reversible) expansion, ∫dQ/T is Q/T, since T is constant. Therefore (from 44.4) the change in entropy is

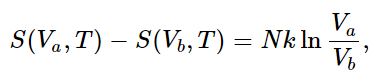
so S(V,T)=N k ln V plus some function of T only. How does S depend on T? We know that for a reversible adiabatic expansion, no heat is exchanged. Thus the entropy does not change even though V changes, provided that T changes also, such that TV^γ−1=constant. Can you see that this implies that

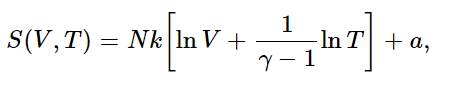
where a is some constant independent of both V and T? [a is called the chemical constant. It depends on the gas in question, and may be determined experimentally from the Nernst theorem by measuring the heat liberated in cooling and condensing the gas until it is brought to a solid (or for helium, a liquid) at 0^∘, by integrating ∫dQ/T. It can also be determined theoretically by means of Planck’s constant and quantum mechanics, but we shall not study it in this course.]

Now we shall remark on some of the properties of the entropy of things. We first remember that if we go along a reversible cycle from a to b, then the entropy of the substance will change by S_b−S_a. And we remember that as we go along the path, the entropy—the heat delivered at unit temperature—increases according to the rule dS=dQ/T, where dQ is the heat we remove from the substance when its temperature is T.

We already know that if we have a reversible cycle, the total entropy of everything is not changed, because the heat Q₁ absorbed at T₁ and the heat Q₂ delivered at T₂ correspond to equal and opposite changes in entropy, so that the net change in the entropy is zero. So for a reversible cycle there is no change in the entropy of anything, including the reservoirs. This rule may look like the conservation of energy again, but it is not; it applies only to reversible cycles. If we include irreversible cycles there is no law of conservation of entropy.

We shall give two examples. First, suppose that we do irreversible work on an object by friction, generating a heat Q on some object at temperature T. The entropy is increased by Q/T. The heat Q is equal to the work, and thus when we do a certain amount of work by friction against an object whose temperature is T, the entropy of the whole world increases by W/T.

Another example of irreversibility is this: If we put together two objects that are at different temperatures, say T₁ and T₂, a certain amount of heat will flow from one to the other by itself. Suppose, for instance, we put a hot stone in cold water. Then when a certain heat ΔQ is transferred from T₁ to T₂, how much does the entropy of the hot stone change? It decreases by ΔQ/T₁. How much does the water entropy change? It increases by ΔQ/T₂. The heat will, of course, flow only from the higher temperature T₁ to the lower temperature T₂, so that ΔQ is positive if T₁ is greater than T₂. So the change in entropy of the whole world is positive, and it is the difference of the two fractions:

So the following proposition is true: in any process that is irreversible, the entropy of the whole world is increased. Only in reversible processes does the entropy remain constant. Since no process is absolutely reversible, there is always at least a small gain in the entropy; a reversible process is an idealization in which we have made the gain of entropy minimal.

Unfortunately, we are not going to enter into the field of thermodynamics very far. Our purpose is only to illustrate the principal ideas involved and the reasons why it is possible to make such arguments, but we will not use thermodynamics very much in this course. Thermodynamics is used very often by engineers and, particularly, by chemists. So we must learn our thermodynamics in practice in chemistry or engineering. Because it is not worthwhile duplicating everything, we shall just give some discussion of the origin of the theory, rather than much detail for special applications.

The two laws of thermodynamics are often stated this way:

First law: the energy of the universe is always constant.

Second law: the entropy of the universe is always increasing.

That is not a very good statement of the second law; it does not say, for example, that in a reversible cycle the entropy stays the same, and it does not say exactly what the entropy is. It is just a clever way of remembering the two laws, but it does not really tell us exactly where we stand. We have summarized the laws discussed in this chapter in Table 44–1. In the next chapter we shall apply these laws to discover the relationship between the heat generated in the expansion of a rubber band, and the extra tension when it is heated.

Table 44–1

Summary of the laws of thermodynamics

First law:

Heat put into a system + Work done on a system = Increase in internal energy of the system:

dQ+dW=dU.

Second law:

A process whose only net result is to take heat from a reservoir and convert it to work is impossible.

No heat engine taking heat Q₁ from T₁ and delivering heat Q₂ at T₂ can do more work than a reversible engine, for which

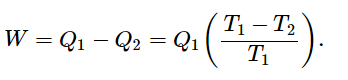
The entropy of a system is defined this way:

(a) If heat ΔQ is added reversibly to a system at temperature T, the increase in entropy of the system is ΔS=ΔQ/T.

(b) At T=0, S=0 (third law).

In a reversible change, the total entropy of all parts of the system (including reservoirs) does not change.

In irreversible change, the total entropy of the system always increases.

مواضيع ذات صلة

الديناميكا الحرارية الجزيئية

توزيع بولتزمان

العلاقات بين الخواص

القانون الثالث للديناميكا الحرارية

الطاقة الحرة

القانون الثاني للديناميكا الحرارية

القانون الأول للديناميكا الحرارية

Order and entropy

Irreversibility

The Clausius-Clapeyron equation

Internal energy

The thermodynamic temperature