Chi-Squared Test
المؤلف:
Kenney, J. F. and Keeping, E. S.
المصدر:
Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
الجزء والصفحة:
...
1-5-2021
2152
Chi-Squared Test
Let the probabilities of various classes in a distribution be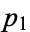 
, 
, ..., 
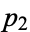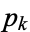, with observed frequencies 
, 
, ..., 
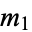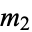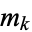. The quantity
 |
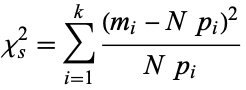(1)
|
is therefore a measure of the deviation of a sample from expectation, where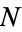 
is the sample size. Karl Pearson proved that the limiting distribution of 
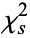is a chi-squared distribution (Kenney and Keeping 1951, pp. 114-116).
The probability that the distribution assumes a value of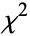 
greater than the measured value 
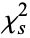is then given by
There are some subtleties involved in using the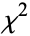 
test to fit curves (Kenney and Keeping 1951, pp. 118-119). When fitting a one-parameter solution using 
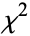, the best-fit parameter value can be found by calculating 
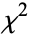at three points, plotting against the parameter values of these points, then finding the minimum of a parabola fit through the points (Cuzzi 1972, pp. 162-168).
REFERENCES:
Cuzzi, J. The Subsurface Nature of Mercury and Mars from Thermal Microwave Emission. Ph.D. Thesis. Pasadena, CA: California Institute of Technology, 1972.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
