Uniform Sum Distribution
المؤلف:
Derbyshire, J.
المصدر:
Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
الجزء والصفحة:
...
16-4-2021
2813
Uniform Sum Distribution
The distribution for the sum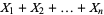 
of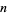 
uniform variates on the interval ![[0,1]](https://mathworld.wolfram.com/images/equations/UniformSumDistribution/Inline3.gif)
can be found directly as
 |
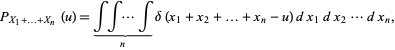(1)
|
where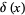 
is a delta function.
A more elegant approach uses the characteristic function to obtain
=1/(2(n-1)!)sum_(k=0)^n(-1)^k(n; k)(u-k)^(n-1)sgn(u-k),](https://mathworld.wolfram.com/images/equations/UniformSumDistribution/NumberedEquation2.gif) |
(2)
|
where the Fourier parameters are taken as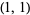 
. The first few values of 
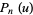are then given by
illustrated above.
Interestingly, the expected number of picks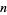 
of a number 
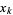from a uniform distribution on ![[0,1]](https://mathworld.wolfram.com/images/equations/UniformSumDistribution/Inline21.gif)
so that the sum 
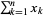exceeds 1 is e (Derbyshire 2004, pp. 366-367). This can be demonstrated by noting that the probability of the sum of 
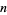variates being greater than 1 while the sum of 
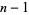variates being less than 1 is
The values for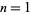 
, 2, ... are 0, 1/2, 1/3, 1/8, 1/30, 1/144, 1/840, 1/5760, 1/45360, ... (OEIS A001048). The expected number of picks needed to first exceed 1 is then simply
 |
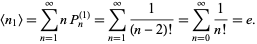(10)
|
It is more complicated to compute the expected number of picks that is needed for their sum to first exceed 2. In this case,
The first few terms are therefore 0, 0, 1/6, 1/3, 11/40, 13/90, 19/336, 1/56, 247/51840, 251/226800, ... (OEIS A090137 and A090138). The expected number of picks needed to first exceed 2 is then simply
The following table summarizes the expected number of picks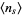 
for the sum to first exceed an integer 
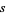(OEIS A089087). A closed form is given by
 |
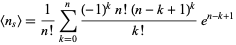(16)
|
(Uspensky 1937, p. 278).
 |
 |
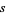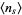OEIS |
approximate |
| 1 |
 |
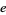A001113 |
2.71828182... |
| 2 |
 |
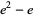A090142 |
4.67077427... |
| 3 |
 |
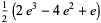A090143 |
6.66656563... |
| 4 |
 |
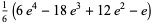A089139 |
8.66660449... |
| 5 |
 |
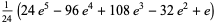A090611 |
10.66666206... |
REFERENCES:
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Sloane, N. J. A. Sequences A001048/M0890, A001113/M1727, A089087, A089139, A090137, A090138, A090142, A090143, and A090611 in "The On-Line Encyclopedia of Integer Sequences."
Uspensky, J. V. Introduction to Mathematical Probability. New York: McGraw-Hill, 1937.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
