Triangular Distribution
المؤلف:
Evans, M.; Hastings, N.; and Peacock, B.
المصدر:
"Triangular Distribution." Ch. 40 in Statistical Distributions, 3rd ed. New York: Wiley
الجزء والصفحة:
pp. 187-188
15-4-2021
2509
Triangular Distribution
The triangular distribution is a continuous distribution defined on the range ![x in [a,b]](https://mathworld.wolfram.com/images/equations/TriangularDistribution/Inline1.gif)
with probability density function
![P(x)=<span style=]() {(2(x-a))/((b-a)(c-a)) for a<=x<=c; (2(b-x))/((b-a)(b-c)) for c<x<=b " src="https://mathworld.wolfram.com/images/equations/TriangularDistribution/NumberedEquation1.gif" style="height:84px; width:222px" /> |
(1)
|
and distribution function
![D(x)=<span style=]() {((x-a)^2)/((b-a)(c-a)) for a<=x<=c; 1-((b-x)^2)/((b-a)(b-c)) for c<x<=b, " src="https://mathworld.wolfram.com/images/equations/TriangularDistribution/NumberedEquation2.gif" style="height:90px; width:250px" /> |
(2)
|
where ![c in [a,b]](https://mathworld.wolfram.com/images/equations/TriangularDistribution/Inline2.gif)
is the mode.
The symmetric triangular distribution on ![[a,b]](https://mathworld.wolfram.com/images/equations/TriangularDistribution/Inline3.gif)
is implemented in the Wolfram Language as TriangularDistribution[a, b], and the triangular distribution on ![[a,b]](https://mathworld.wolfram.com/images/equations/TriangularDistribution/Inline4.gif)
with mode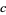 
as TriangularDistribution[a, b, c].
The mean is
 |
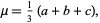(3)
|
the raw moments are
and the central moments are
It has skewness and kurtosis excess given by
EFERENCES:
Evans, M.; Hastings, N.; and Peacock, B. "Triangular Distribution." Ch. 40 in Statistical Distributions, 3rd ed. New York: Wiley, pp. 187-188, 2000.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
