Random Walk--1-Dimensional
Let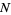 
steps of equal length be taken along a line. Let 
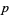be the probability of taking a step to the right, 
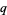the probability of taking a step to the left, 
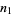the number of steps taken to the right, and 
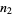the number of steps taken to the left. The quantities 
, 
, 
, 
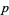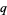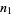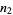, and 
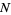are related by
 |
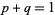(1)
|
and
 |
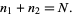(2)
|
Now examine the probability of taking exactly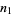 
steps out of 
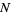to the right. There are 
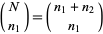ways of taking 
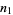steps to the right and 
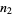to the left, where 
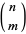is a binomial coefficient. The probability of taking a particular ordered sequence of 
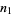and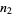 
steps is 
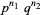. Therefore,
 |
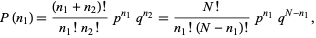(3)
|
where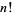 
is a factorial. But this is simply a binomial distribution, so the mean number of steps 
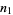to the right is
 |
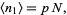(4)
|
and the mean number of steps to the left is
 |
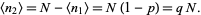(5)
|
Similarly, the variance is given by
 |
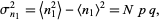(6)
|
and the root-mean-square deviation is
 |
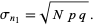(7)
|
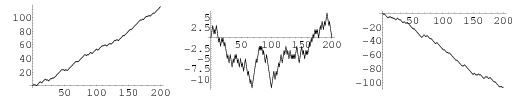
Consider now the distribution of the distances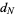 
traveled after a given number of steps,
 |
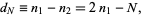(8)
|
as opposed to the number of steps in a given direction. The above plots show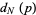 
for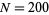 
and three values 
, 
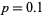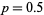, and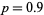 
, respectively. Clearly, weighting the steps toward one direction or the other influences the overall trend, but there is still a great deal of random scatter, as emphasized by the plot below, which shows three random walks all with 
.
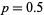Surprisingly, the most probable number of sign changes in a walk is 0, followed by 1, then 2, etc.
For a random walk with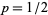 
, the probability 
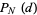of traveling a given distance 
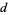after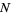 
steps is given in the following table.
| steps |
 |
 |
 |
 |
 |
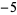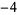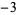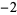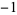0 |
1 |
2 |
3 |
4 |
5 |
| 0 |
|
|
|
|
|
1 |
|
|
|
|
|
| 1 |
|
|
|
|
 |
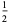0 |
 |
|
|
|
|
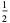| 2 |
|
|
|
 |
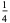0 |
 |
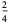0 |
 |
|
|
|
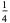| 3 |
|
|
 |
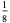0 |
 |
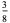0 |
 |
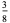0 |
 |
|
|
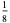| 4 |
|
 |
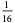0 |
 |
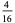0 |
 |
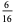0 |
 |
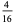0 |
 |
|
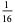| 5 |
 |
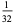0 |
 |
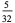0 |
 |
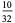0 |
 |
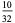0 |
 |
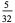0 |
 |
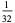In this table, subsequent rows are found by adding half of each cell in a given row to each of the two cells diagonally below it. In fact, it is simply Pascal's triangle padded with intervening zeros and with each row multiplied by an additional factor of 1/2. The coefficients in this triangle are given by
 |
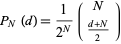(9)
|
(Papoulis 1984, p. 291). The moments
 |
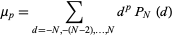(10)
|
of this distribution of signed distances are then given by
so the mean is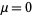 
, the skewness is 
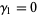, and the kurtosis excess is
 |
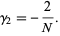(15)
|
The expectation value of the absolute distance after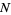 
steps is therefore given by
This sum can be done symbolically by separately considering the cases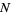 
even and 
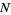odd. First, consider even 
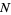so that 
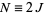. Then
But this sum can be evaluated analytically as
 |
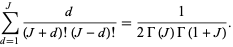(22)
|
Writing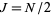 
, plugging back in, and simplifying gives
 |
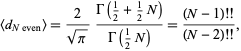(23)
|
where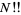 
is the double factorial.
Now consider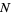 
odd, so 
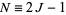. Then
But this sum can be evaluated analytically as
![sum_(d=1)^J(2d-1)/((J+d-1)!(J-d)!)=1/([Gamma(J)]^2).](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/NumberedEquation14.gif) |
(29)
|
Writing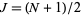 
, plugging back in, and simplifying gives
Both the even and odd solutions can be written in terms of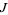 
as
 |
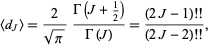(33)
|
or explicitly in terms of 
as
The first few values of 
for 
, 1, ... are therefore 0, 1, 1, 3/2, 3/2, 15/8, 15/8, 35/16, 35/16, ... (OEIS A086116 and A060818; Abramowitz and Stegun 1972, Prévost 1933, Hughes 1995), where the terms of each pair are given by the generating function
 |
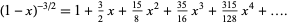(36)
|
These numbers also arise in the heads-minus-tails distribution.
Now, examine the asymptotic behavior of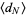 
. The asymptotic expansion of the gamma function ratio is
 |
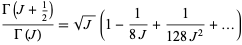(37)
|
(Graham et al. 1994), so plugging in the expression for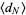 
gives the asymptotic series
 |
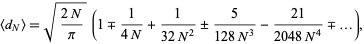(38)
|
where the top signs are taken for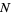 
even and the bottom signs for 
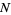odd. Therefore, for large 
,
 |
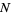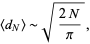(39)
|
which is also shown by Grünbaum (1960), Mosteller et al. (1961, p. 14), and König et al. (1999).
Tóth (2000) has proven that there are no more than three most-visited sites in a simple symmetric random walk in one dimension with unit steps.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 798, 1972.
Chandrasekhar, S. "Stochastic Problems in Physics and Astronomy." Rev. Modern Phys. 15, 1-89, 1943. Reprinted in Selected Papers on Noise and Stochastic Processes (Ed. N. Wax). New York: Dover, pp. 3-91, 1954.
Erdős, P. and Révész, P. "On the Favourite Points of Random Walks." Math. Structures--Comput. Math.--Math. Model. (Sofia) 2, 152-157, 1984.
Erdős, P. and Révész, P. "Problems and Results on Random Walks." In Mathematical Statistics and Probability Theory, Vol. B: Statistical Inference and Methods. Proceedings of the Sixth Pannonian Symposium on Mathematical Statistics Held in Bad Tatzmannsdorf, September 14-20, 1986 (Ed. P. Bauer, F. Koneczny, and W. Wertz). Dordrecht, Netherlands: Reidel, pp. 59-65, 1987.
Feller, W. Ch. 3 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed., rev. printing. New York: Wiley, 1968.
Gardner, M. "Random Walks and Gambling." Ch. 6 in Mathematical Circus: More Puzzles, Games, Paradoxes, and Other Mathematical Entertainments. Washington, DC: Math. Assoc. Amer., pp. 66-74, 1992.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Answer to problem 9.60 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Grünbaum, B. "Projection Constants." Trans. Amer. Math. Soc. 95, 451-465, 1960.
Hersh, R. and Griego, R. J. "Brownian Motion and Potential Theory." Sci. Amer. 220, 67-74, 1969.
Hughes, B. D. Eq. (7.282) in Random Walks and Random Environments, Vol. 1: Random Walks. New York: Oxford University Press, p. 513, 1995.
Kac, M. "Random Walk and the Theory of Brownian Motion." Amer. Math. Monthly 54, 369-391, 1947. Reprinted in Selected Papers on Noise and Stochastic Processes (Ed. N. Wax). New York: Dover, pp. 295-317, 1954.
König, H.; Schütt, C.; and Tomczak-Jaegermann, N. "Projection Constants of Symmetric Spaces and Variants of Khintchine's Inequality." J. reine angew. Math. 511, 1-42, 1999.
Mosteller, F.; Rourke, R. E. K.; and Thomas, G. B. Probability and Statistics. Reading, MA: Addison-Wesley, 1961.
Papoulis, A. "Random Walk." Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 290-291, 1984.
Prévost, G. Tables de Fonctions Sphériques. Paris: Gauthier-Villars, pp. 156-157, 1933.
Révész, P. Random Walk in Random and Non-Random Environment. Singapore: World Scientific, 1990.
Sloane, N. J. A. Sequences A060818 and A086116 in "The On-Line Encyclopedia of Integer Sequences."
Tóth, B. "No More than Three Favourite Sites for Simple Random Walk." 26 Apr 2000. https://arxiv.org/abs/math.PR/0004164.
Tóth, B. and Werner, W. "Tied Favourite Edges for Simple Random Walk." Combin., Prob., Comput. 6, 359-369, 1997.
Trott, M. "The Mathematica Guidebooks Additional Material: Random Walk with Varying Step Size." https://www.mathematicaguidebooks.org/additions.shtml#N_1_01.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
