

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Random Matrix
المؤلف:
Bougerol, P. and Lacroix, J.
المصدر:
Random Products of Matrices with Applications to Schrödinger Operators. Basel, Switzerland: Birkhäuser 1985.
الجزء والصفحة:
...
21-3-2021
4153
Random Matrix
A random matrix is a matrix of given type and size whose entries consist of random numbers from some specified distribution.
Random matrix theory is cited as one of the "modern tools" used in Catherine's proof of an important result in prime number theory in the 2005 film Proof.
For a real 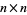 matrix with elements having a standard normal distribution, the expected number of real eigenvalues is given by
matrix with elements having a standard normal distribution, the expected number of real eigenvalues is given by
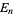 |
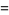 |
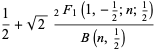 |
(1) |
 |
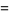 |
(2) |
where 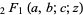 is a hypergeometric function and
is a hypergeometric function and 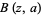 is a beta function (Edelman et al. 1994, Edelman and Kostlan 1994).
is a beta function (Edelman et al. 1994, Edelman and Kostlan 1994). 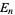 has asymptotic behavior
has asymptotic behavior
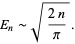 |
(3) |
Let 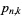 be the probability that there are exactly
be the probability that there are exactly 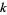 real eigenvalues in the complex spectrum of the
real eigenvalues in the complex spectrum of the 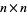 matrix. Edelman (1997) showed that
matrix. Edelman (1997) showed that
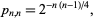 |
(4) |
which is the smallest probability of all 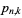 s. The entire probability function of the number of expected real eigenvalues in the spectrum of a Gaussian real random matrix was derived by Kanzieper and Akemann (2005) as
s. The entire probability function of the number of expected real eigenvalues in the spectrum of a Gaussian real random matrix was derived by Kanzieper and Akemann (2005) as
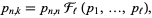 |
(5) |
where
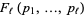 |
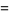 |
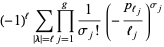 |
(6) |
 |
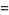 |
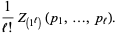 |
(7) |
In (6), the summation runs over all partitions 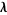 of length
of length 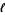 ,
, 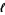 is the number of pairs of complex-conjugated eigenvalues, and
is the number of pairs of complex-conjugated eigenvalues, and 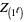 are zonal polynomial. In addition, (6) makes use a frequency representation of the partition
are zonal polynomial. In addition, (6) makes use a frequency representation of the partition 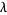 (Kanzieper and Akemann 2005). The arguments
(Kanzieper and Akemann 2005). The arguments 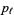 depend on the parity of
depend on the parity of 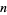 (the matrix dimension) and are given by
(the matrix dimension) and are given by
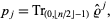 |
(8) |
where 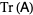 is a matrix trace,
is a matrix trace, 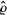 is an
is an 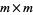 matrix with entries
matrix with entries
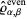 |
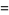 |
![int_0^inftyy^(2(beta-alpha)-1)e^(y^2)erfc(ysqrt(2))×[(2alpha+1)L_(2alpha+1)^(2(beta-alpha)-1)(-2y^2)+2y^2L_(2alpha-1)^(2(beta-alpha)+1)(-2y^2)]dy](https://mathworld.wolfram.com/images/equations/RandomMatrix/Inline33.gif) |
(9) |
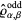 |
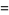 |
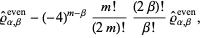 |
(10) |
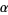 and
and 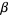 vary between 0 and
vary between 0 and 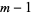 ,
, 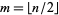 with
with 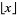 the floor function),
the floor function), 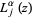 are generalized Laguerre polynomials, and
are generalized Laguerre polynomials, and 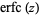 is the complementary erf function erfc (Kanzieper and Akemann 2005).
is the complementary erf function erfc (Kanzieper and Akemann 2005).
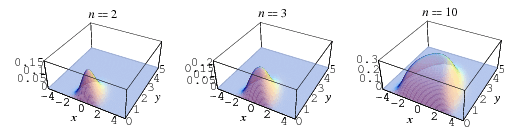
Edelman (1997) proved that the density of a random complex pair of eigenvalues 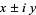 of a real
of a real 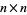 matrix whose elements are taken from a standard normal distribution is
matrix whose elements are taken from a standard normal distribution is
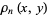 |
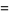 |
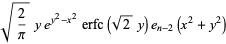 |
(11) |
 |
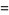 |
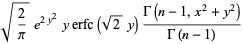 |
(12) |
for 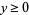 , where
, where 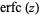 is the erfc (complementary error) function,
is the erfc (complementary error) function, 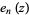 is the exponential sum function, and
is the exponential sum function, and 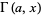 is the upper incomplete gamma function. Integrating over the upper half-plane (and multiplying by 2) gives the expected number of complex eigenvalues as
is the upper incomplete gamma function. Integrating over the upper half-plane (and multiplying by 2) gives the expected number of complex eigenvalues as
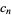 |
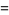 |
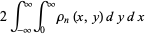 |
(13) |
 |
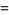 |
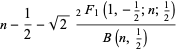 |
(14) |
 |
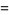 |
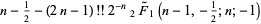 |
(15) |
(Edelman 1997). The first few values are
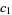 |
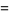 |
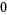 |
(16) |
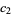 |
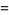 |
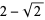 |
(17) |
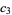 |
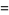 |
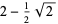 |
(18) |
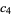 |
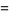 |
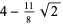 |
(19) |
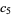 |
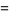 |
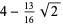 |
(20) |
(OEIS A052928, A093605, and A046161).
Girko's circular law considers eigenvalues 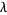 (possibly complex) of a set of random
(possibly complex) of a set of random 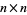 real matrices with entries independent and taken from a standard normal distribution and states that as
real matrices with entries independent and taken from a standard normal distribution and states that as 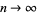 ,
, 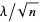 is uniformly distributed on the unit disk in the complex plane.
is uniformly distributed on the unit disk in the complex plane.
Wigner's semicircle law states that the for large 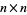 symmetric real matrices with elements taken from a distribution satisfying certain rather general properties, the distribution of eigenvalues is the semicircle function.
symmetric real matrices with elements taken from a distribution satisfying certain rather general properties, the distribution of eigenvalues is the semicircle function.
If 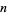 matrices
matrices 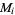 are chosen with probability 1/2 from one of
are chosen with probability 1/2 from one of
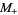 |
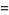 |
![[0 1; 1 1]](https://mathworld.wolfram.com/images/equations/RandomMatrix/Inline89.gif) |
(21) |
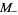 |
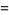 |
![[0 1; 1 -1],](https://mathworld.wolfram.com/images/equations/RandomMatrix/Inline92.gif) |
(22) |
then
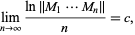 |
(23) |
where 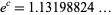 (OEIS A078416) and
(OEIS A078416) and 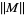 denotes the matrix spectral norm (Bougerol and Lacroix 1985, pp. 11 and 157; Viswanath 2000). This is the same constant appearing in the random Fibonacci sequence. The following Wolfram Language code can be used to estimate this constant.
denotes the matrix spectral norm (Bougerol and Lacroix 1985, pp. 11 and 157; Viswanath 2000). This is the same constant appearing in the random Fibonacci sequence. The following Wolfram Language code can be used to estimate this constant.
With[{n = 100000},
m = Fold[Dot, IdentityMatrix[2],
{{0, 1}, {1, #}}& /@
RandomChoice[{-1, 1}, {n}]
] // N;
Log[Sqrt[Max[Eigenvalues[Transpose[m] . m]]]] /
n
]
REFERENCES:
Bougerol, P. and Lacroix, J. Random Products of Matrices with Applications to Schrödinger Operators. Basel, Switzerland: Birkhäuser 1985.
Chassaing, P.; Letac, G.; and Mora, M. "Brocot Sequences and Random Walks on 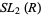 ." In Probability Measures on Groups VII (Ed. H. Heyer). New York Springer-Verlag, pp. 36-48, 1984.
." In Probability Measures on Groups VII (Ed. H. Heyer). New York Springer-Verlag, pp. 36-48, 1984.
Edelman, A. "The Probability that a Random Real Gaussian Matrix has 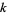 Real Eigenvalues, Related Distributions, and the Circular Law." J. Multivariate Anal. 60, 203-232, 1997.
Real Eigenvalues, Related Distributions, and the Circular Law." J. Multivariate Anal. 60, 203-232, 1997.
Edelman, A. and Kostlan, E. "How Many Zeros of a Random Polynomial are Real?" Bull. Amer. Math. Soc. 32, 1-37, 1995.
Edelman, A.; Kostlan, E.; and Shub, M. "How Many Eigenvalues of a Random Matrix are Real?" J. Amer. Math. Soc. 7, 247-267, 1994.
Furstenberg, H. "Non-Commuting Random Products." Trans. Amer. Math. Soc. 108, 377-428, 1963.
Furstenberg, H. and Kesten, H. "Products of Random Matrices." Ann. Math. Stat. 31, 457-469, 1960.
Girko, V. L. Theory of Random Determinants. Boston, MA: Kluwer, 1990.
Kanzieper, E. and Akemann, G. "Statistics of Real Eigenvalues in Ginibre's Ensemble of Random Real Matrices." Phys. Rev. Lett. 95, 230201-1-230201-4, 2005.
Katz, M. and Sarnak, P. Random Matrices, Frobenius Eigenvalues, and Monodromy. Providence, RI: Amer. Math. Soc., 1999.
Lehmann, N. and Sommers, H.-J. "Eigenvalue Statistics of Random Real Matrices." Phys. Rev. Let. 67, 941-944, 1991.
Mehta, M. L. Random Matrices, 3rd ed. New York: Academic Press, 1991.
Sloane, N. J. A. Sequences A046161, A052928, A078416, and A093605 in "The On-Line Encyclopedia of Integer Sequences."
Viswanath, D. "Random Fibonacci Sequences and the Number 1.13198824...." Math. Comput. 69, 1131-1155, 2000.
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















