
Stochastic Matrix
 المؤلف:
Poole, D. G.
المؤلف:
Poole, D. G.
 المصدر:
"The Stochastic Group." Amer. Math. Monthly 102,
المصدر:
"The Stochastic Group." Amer. Math. Monthly 102,
 الجزء والصفحة:
798-801
الجزء والصفحة:
798-801
 18-2-2021
18-2-2021
 1672
1672
Stochastic Matrix
A stochastic matrix, also called a probability matrix, probability transition matrix, transition matrix, substitution matrix, or Markov matrix, is matrix used to characterize transitions for a finite Markov chain, Elements of the matrix must be real numbers in the closed interval [0, 1].
A completely independent type of stochastic matrix is defined as a square matrix with entries in a field 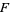 such that the sum of elements in each column equals 1. There are two nonsingular
such that the sum of elements in each column equals 1. There are two nonsingular 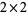 stochastic matrices over
stochastic matrices over 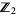 (i.e., the integers mod 2),
(i.e., the integers mod 2),
There are six nonsingular stochastic 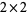 matrices over
matrices over 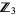 ,
,
In fact, the set 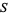 of all nonsingular stochastic
of all nonsingular stochastic 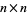 matrices over a field
matrices over a field 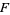 forms a group under matrix multiplication. This group is called the stochastic group.
forms a group under matrix multiplication. This group is called the stochastic group.
The following tables give the number of distinct stochastic matrices (and distinct nonsingular stochastic matrices) over 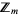 for small
for small 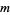 .
.
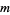 |
stochastic 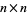 matrices over matrices over 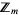 |
| 2 |
1, 4, 64, 4096, ... |
| 3 |
1, 9, 729, ... |
| 4 |
1, 16, 4096, ... |
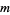 |
stochastic nonsingular 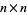 matrices over matrices over 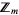 |
| 2 |
1, 2, 24, 1440, ... |
| 3 |
1, 6, 450, ... |
| 4 |
1, 12, 3108, ... |
REFERENCES:
Poole, D. G. "The Stochastic Group." Amer. Math. Monthly 102, 798-801, 1995.
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


