Magnetic Flux

In our discussion of velocity fields and electric fields, we used the concept of the flux of a field. For the velocity field, the flux Φ_v of water was the volume of water flowing per second past some perpendicular area A_⊥ . For a uniform stream moving at a speed v, the flux was Φ_v = vA_⊥. For the electric field, the formula for flux was Φ_E = EA_⊥.
In Figures (1 and 2), we have a magnetic field that "flows" through a wire loop. Following the same convention that we used for velocity and electric fields, we will define the magnetic flux Φ_B as the strength of the field B times the perpendicular area A_⊥ through which the field is flowing

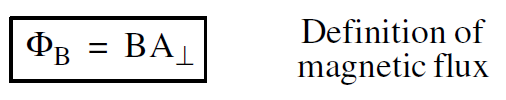.........(1)

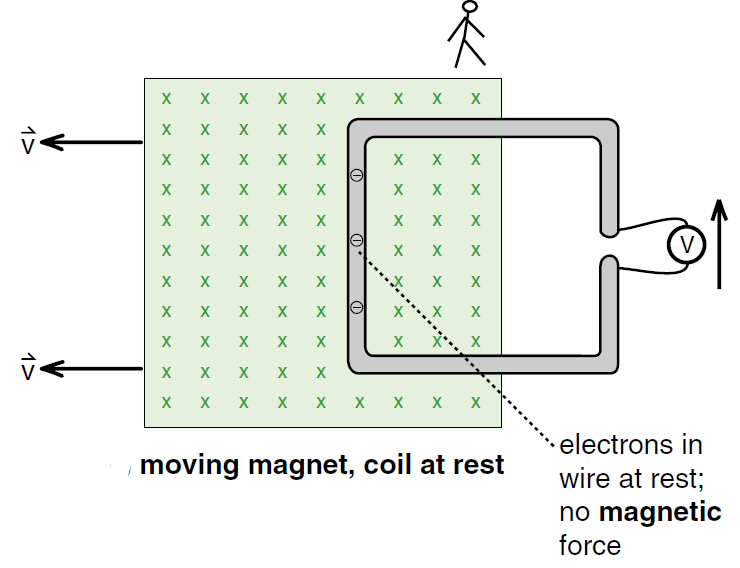
Figure 1.

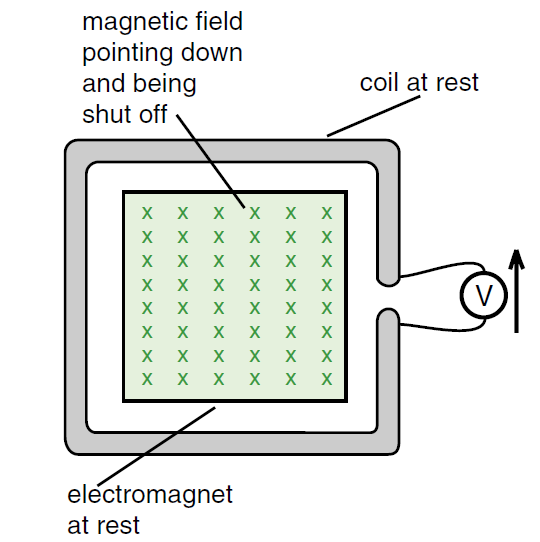
Figure 2: Here we have a large coil that lies completely outside the magnetic field. Thus there is no magnetic force on any of the electrons in the coil wire. Yet when we turn the magnet on or off, we get a reading in the volt meter.

In both figures (1) and (2), the flux Φ_B through the wire loop is decreasing. In Figure (1), Φ_B decreases because the perpendicular area A_⊥ is decreasing as the loop and the magnet move apart. In Figure (2), the flux Φ_B is decreasing because B is being shut off. The important observation is that whenever the flux Φ_B through the loop decreases, whatever the reason for the change may be, we get a voltage reading V on the voltmeter.

مواضيع ذات صلة

عجائب المجالات المغناطيسية

المجال المغناطيسي الارضي

Planetary magnetism

Therapy and treatment

Cellular biology

Magnetotaxis

Magnetic field effects

Electrodeposition

Magnetic memory

Materials for spin electronics

Actuators

Sensors