Helmholtz Differential Equation--Spherical Surface
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
المرجع الالكتروني للمعلوماتيه
الجزء والصفحة:
...
18-7-2018
1901
Helmholtz Differential Equation--Spherical Surface
On the surface of a sphere, attempt separation of variables in spherical coordinates by writing
 |
(1)
|
then the Helmholtz differential equation becomes
 |
(2)
|
Dividing both sides by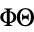 
,
 |
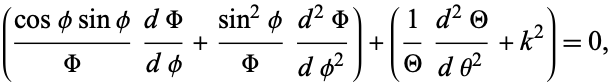(3)
|
which can now be separated by writing
 |
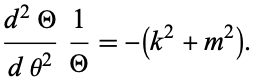(4)
|
The solution to this equation must be periodic, so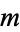 
must be an integer. The solution may then be defined either as a complex function
 |
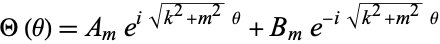(5)
|
for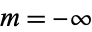 
, ..., 
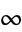, or as a sum of real sine and cosine functions
 |
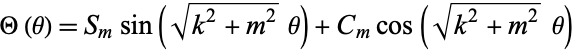(6)
|
for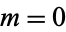 
, ..., 
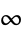. Plugging (4) into (3) gives
 |
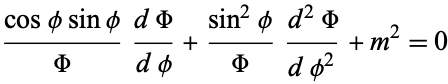(7)
|
 |
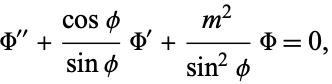(8)
|
which is the Legendre differential equation for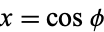 
with
 |
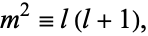(9)
|
giving
 |
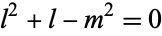(10)
|
 |
(11)
|
Solutions are therefore Legendre polynomials with a complex index. The general complex solution is then
 |
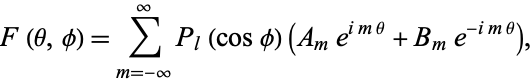(12)
|
and the general real solution is
 |
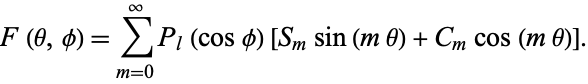(13)
|
Note that these solutions depend on only a single variable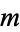 
. However, on the surface of a sphere, it is usual to express solutions in terms of the spherical harmonics derived for the three-dimensional spherical case, which depend on the two variables 
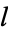and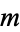 
.
الاكثر قراءة في المعادلات التفاضلية الجزئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
