


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 14-9-2016
Date: 19-6-2019
Date: 23-2-2017
|
The tetrahedral crystal field
So far we have restricted the discussion to octahedral complexes; we now turn to the tetrahedral crystal field. Figure 1.1 shows a convenient way of relating a tetrahedron to a Cartesian axis set. With the complex in this orientation, none of the metal d orbitals points exactly at the ligands, but the dxy, dyz and dxz orbitals come nearer to doing so than the dz2 and dx2-y2 orbitals. For a regular tetrahedron, the splitting of the d orbitals is inverted compared with that for a regular octahedral structure, and the energy difference (Δtet) is smaller.

Fig. 1.1 The relationship between a tetrahedral ML4 complex and a cube; the cube is readily related to a Cartesian axis set. The ligands lie between the x, y and z axes; compare this with an octahedral complex, where the ligands lie on the axes.
If all other things are equal (and of course, they never are), the relative splittings Δoct and Δtet are related by equation 1.1.
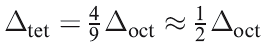 (1.1)
(1.1)
Figure 1.2 compares crystal field splitting for octahedral and tetrahedral fields; remember, the subscript g in the symmetry labels is not needed in the tetrahedral case.
Since Δtet is significantly smaller than Δoct , tetrahedral complexes are high-spin. Also, since smaller amounts of energy are needed for an t2←e transition (tetrahedral) than for an eg←t2g transition (octahedral), corresponding octahedral and tetrahedral complexes often have different colours. Jahn–Teller effects in tetrahedral complexes are illustrated by distortions in d9 (e.g. [CuCl4]2-) and high-spin d4 complexes. A particularly strong structural distortion is observed in [FeO4]4-.
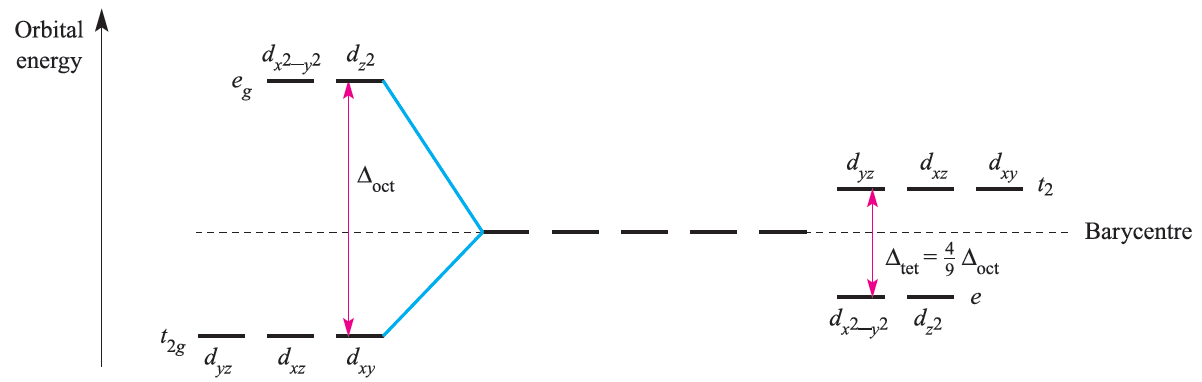
Fig. 1.2 Crystal field splitting diagrams for octahedral (left-hand side) and tetrahedral (right-hand side) fields.


|
|
|
|
مقاومة الأنسولين.. أعراض خفية ومضاعفات خطيرة
|
|
|
|
|
|
|
أمل جديد في علاج ألزهايمر.. اكتشاف إنزيم جديد يساهم في التدهور المعرفي ؟
|
|
|
|
|
|
|
العتبة العباسية المقدسة تجري القرعة الخاصة بأداء مناسك الحج لمنتسبيها
|
|
|