A tale from St Ives

Children can start combinatorics at a tender age. One traditional nursery rhyme poses a combinatorial question:

As I was going to St Ives,
I met a man with seven wives;
Every wife had seven sacks,
Every sack had seven cats,
Every cat had seven kits.
Kits, cats, sacks and wives,
How many were going to St Ives?

The last line contains the trick question. An implicit assumption is that the narrator is the only person on his way ‘to’ St Ives, so the answer is ‘one’. Some people exclude the narrator and for them the answer would be ‘none’.

The charm of the poem lies in its ambiguity and the various questions it can generate. We could ask: how many were coming from St Ives? Again interpretation is important. Can we be sure the man with his seven wives were all travelling away from St Ives? Were the wives accompanying the man when he was met, or were they somewhere else? The first requirement of a combinatorial problem is that assumptions be agreed beforehand.

We’ll assume the entourage was coming along the single road away from the Cornish seaside town and that the ‘kits, cats, sacks and wives’ were all present. How many were there coming from St Ives? The following table gives us a solution.

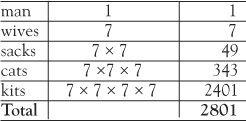
In 1858 Alexander Rhind a Scottish antiquarian visiting Luxor came across a 5 metre long papyrus filled with Egyptian mathematics from the period 1800 BC. He bought it. A few years later it was acquired by the British Museum and its hieroglyphics translated. Problem 79 of the Rhind Papyrus is a problem of houses, cats, mice and wheat very similar to the kits, cats, sacks and wives of St Ives. Both involve powers of 7 and the same kind of analysis. Combinatorics, it seems, has a long history.

Factorial numbers

The problem of queues introduces us to the first weapon in the combinatorial armoury – the factorial number. Suppose Alan, Brian, Charlotte, David, and Ellie form themselves into a queue

E   C   A    B   D

with Ellie at the head of the queue followed by Charlotte, Alan and Brian with David at the end. By swapping the people around other queues are formed; how many different queues are possible?

The art of counting in this problem depends on choice. There are 5 choices for who we place as the first person in the queue, and once this person has been chosen, there are 4 choices for the second person, and so on. When we come to the last position there is no choice at all as it can only be filled by the person left over. There are therefore 5 × 4 × 3 × 2 × 1 = 120 possible queues. If we started with 6 people, the number of different queues would be 6 × 5 × 4 × 3 × 2 × 1 = 720 and for 7 people there would be 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040 possible queues.

A number obtained by multiplying successive whole numbers is called a factorial number. These occur so often in mathematics that they are written using the notation 5! (read ‘5 factorial’) instead of 5 × 4 × 3 × 2 × 1. Let’s take a look at the first few factorials (we’ll define 0! to equal 1). Straightaway, we see that quite ‘small’ configurations give rise to ‘large’ factorial numbers. The number n may be small but n! can be huge.

If we’re still interested in forming queues of 5 people, but can now draw on a pool of 8 people A,B, C, D, E, F, G, and H, the analysis is almost the same. There are 8 choices for the front person in the queue, 7 for the second and so on. But this time there are 4 choices for the last slot. The number of possible queues is

8 × 7 × 6 × 5 × 4 = 6720

This can be written with the notation for factorial numbers, because

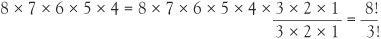
Combinations

In a queue the order matters. The two queues number factorial

C  E  B  A  D                       D  A  C  E  B

are made from the same letters but are different queues. We already know there are 5! queues that can be made with these letters. If we’re interested in counting the ways of selecting 5 people from 8 immaterial of order we must divide 8 × 7 × 6 × 5 × 4 = 6720 by 5!. The number of ways of selecting 5 people from 8 is therefore

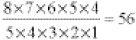
This number, using C for combination, is written ⁸C₅ and is

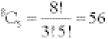
In the UK National Lottery the rules require a selection of 6 numbers from a possible 49 – how many possibilities are there?

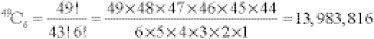
Only one combination wins so there is approximately 1 chance in 14 million of picking the jackpot.

Kirkman’s problem

Combinatorics is a wide field and, though old, it has rapidly developed over the past 40 years, due to its relevance to computer science. Problems involving graph theory, Latin squares and the like can be thought of as part of modern combinatorics.

The essence of combinatorics is captured by a master of the subject, Rev. Thomas Kirkman, working at a time when combinatorics was mostly linked to recreational mathematics. He made many original contributions to discrete geometry, group theory and combinatorics but never had a university appointment. The conundrum which reinforced his reputation as a nononsense mathematician was the one for which he will always be known. In 1850 Kirkman introduced the ‘15 schoolgirls problem’, in which schoolgirls walk to church in 5 rows of 3 on each day of the week. If you are bored with Sudoku you might try to solve it. We need to organize a daily schedule so that no two walk together more than once. Using lower case and upper case deliberately, the girls are: abigail, beatrice, constance, dorothy, emma, frances, grace, Agnes, Bernice, Charlotte, Danielle, Edith, Florence, Gwendolyn and Victoria, labelled a, b, c, d, e, f, g, A, B, C, D, E, F, G and V, respectively.

There are actually seven distinct solutions to Kirkman’s problem, and the one we’ll give is ‘cyclic’ – it is generated by ‘going around’. This is where the labelling of the schoolgirls comes into its own.

It is called cyclic since on each subsequent day the walking schedule is changed from a to b, b to c, down to g to a. The same applies to the upper-case girls A to B, B toC, and so on, but Victoria remains unmoved.

The underlying reason for the choice of notation is that the rows correspond to lines in the Fano geometry . Kirkman’s problem isn’t only a parlour game but one that’s part of mainstream mathematics.

the condensed idea

How many combinations?