Brocard's Problem 

Brocard's problem asks to find the values of 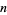 for which  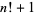is a square number 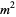, where  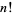is the factorial (Brocard 1876, 1885). The only known solutions are 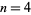, 5, and 7. Pairs of numbers  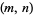are called Brown numbers. In 1906, Gérardin claimed that, if 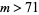, then  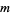must have at least 20 digits. Unaware of Brocard's query, Ramanujan considered the same problem in 1913. Gupta (1935) stated that calculations of  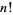up to 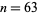 gave no further solutions.

It is virtually certain that there are no more solutions (Guy 1994). In fact, Dabrowski (1996) has shown that 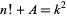 has only finitely many solutions for general 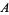, although this result requires assumption of a weak form of the abc conjecture if  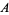is square).

There are no other solutions with 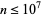 (Wells 1986, p. 70), and Berndt and Galway have further searched up to  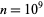without finding any further solutions.

Wilson has also computed the least 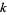 such that  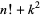is square starting at 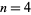, giving 1, 1, 3, 1, 9, 27, 15, 18, 288, 288, 420, 464, 1856, ... (OEIS A038202).

REFERENCES:

Berndt, B. C. and Galway, W. F. "On the Brocard-Ramanujan Diophantine Equation 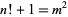." Submitted. http://www.math.uiuc.edu/~galway/Submissions/Ramanujan469.ps and http://www.math.uiuc.edu/~berndt/articles/galway.pdf.

Brocard, H. Question 166. Nouv. Corres. Math. 2, 287, 1876.

Brocard, H. Question 1532. Nouv. Ann. Math. 4, 391, 1885.

Dabrowski, A. "On the Diophantine Equation 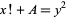." Nieuw Arch. Wisk. 14, 321-324, 1996.

Erdős, P. and Obláth, R. "Über diophantische Gleichungen der Form 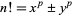 und 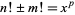." Acta Szeged 8, 241-255, 1937.

Gupta, H. "On a Brocard-Ramanujan Problem." Math. Student 3, 71, 1935.

Guy, R. K. "Equations Involving Factorial 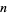." §D25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 193-194, 1994.

Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., p. 327, 2000.

Overholt, M. "The Diophantine Equation 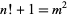." Bull. London Math. Soc. 25, 104, 1993.

Sloane, N. J. A. Sequence A038202 in "The On-Line Encyclopedia of Integer Sequences."

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 57 and 70, 1986.