Foias Constant

A problem listed in a fall issue of Gazeta Matematică in the mid-1970s posed the question if 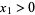 and

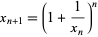(1)

for 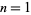, 2, ..., then are there any values for which 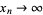? The problem, listed as one given on an entrance exam to prospective freshman in the mathematics department at the University of Bucharest, was solved by C. Foias.

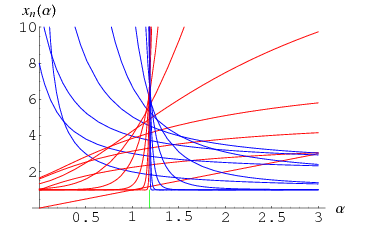
It turns out that there exists exactly one real number

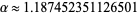(2)

(OEIS A085848) such that if 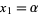, then 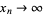. However, no analytic form is known for this constant, either as the root of a function or as a combination of other constants. Moreover, in this case,

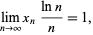(3)

which can be rewritten as

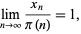(4)

where 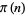 is the prime counting function. However, Ewing and Foias (2000) believe that this connection with the prime number theorem is fortuitous.

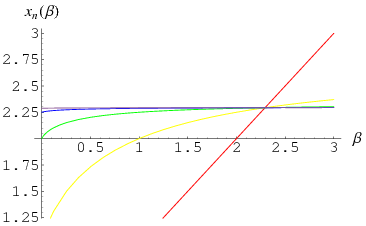
Foias also discovered that the problem stated in the journal was a misprint of the actual exam problem, which used the recurrence 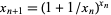 (Ewing and Foias 2000). In this form, the recurrence converges to

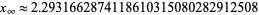(5)

(OEIS A085846), which is simply the root of

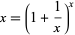(6)

for all starting values of .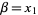

REFERENCES:

Ewing, J. and Foias, C. "An Interesting Serendipitous Real Number." In Finite versus Infinite: Contributions to an Eternal Dilemma (Ed. C. Caluse and G. Păun). London: Springer-Verlag, pp. 119-126, 2000.

Sloane, N. J. A. Sequences A085846 and A085848 in "The On-Line Encyclopedia of Integer Sequences."