


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-5-2018
Date: 13-6-2018
Date: 13-6-2018
|
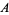 (the growth rate of prey),
(the growth rate of prey), 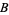 (the rate at which predators destroy prey),
(the rate at which predators destroy prey), 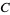 (the death rate of predators), and
(the death rate of predators), and 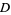 (the rate at which predators increase by consuming prey), the following conditions hold.
(the rate at which predators increase by consuming prey), the following conditions hold.
1. A prey population  increases at a rate
increases at a rate 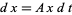 (proportional to the number of prey) but is simultaneously destroyed by predators at a rate
(proportional to the number of prey) but is simultaneously destroyed by predators at a rate 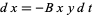 (proportional to the product of the numbers of prey and predators).
(proportional to the product of the numbers of prey and predators).
2. A predator population 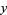 decreases at a rate
decreases at a rate 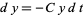 (proportional to the number of predators), but increases at a rate
(proportional to the number of predators), but increases at a rate 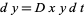 (again proportional to the product of the numbers of prey and predators).
(again proportional to the product of the numbers of prey and predators).
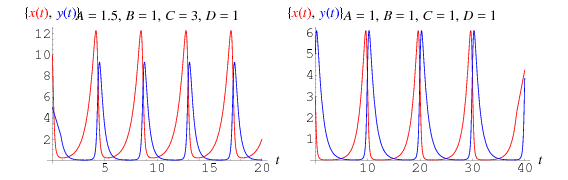
This gives the coupled differential equations
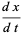 |
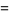 |
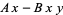 |
(1) |
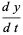 |
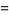 |
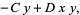 |
(2) |
solutions of which are plotted above, where prey are shown in red, and predators in blue. In this sort of model, the prey curve always lead the predator curve.
Critical points occur when 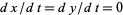 , so
, so
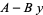 |
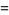 |
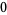 |
(3) |
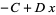 |
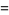 |
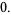 |
(4) |
The sole stationary point is therefore located at 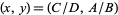 .
.
REFERENCES:
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 5th ed. New York: Wiley, p. 494, 1992.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 135, 1997.



|
|
|
|
لشعر لامع وكثيف وصحي.. وصفة تكشف "سرا آسيويا" قديما
|
|
|
|
|
|
|
كيفية الحفاظ على فرامل السيارة لضمان الأمان المثالي
|
|
|
|
|
|
|
العتبة العباسية المقدسة تجري القرعة الخاصة بأداء مناسك الحج لمنتسبيها
|
|
|