المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Digit Product |
 811
 04:29 مساءً
date: 10-11-2020 |
Author : Allouche, J.-P. and Cohen, H. 
Book or Source : "Dirichlet Series and Curious Infinite Products." Bull. London Math. Soc. 17 
Page and Part : ...|
Read More
Date: 20-10-2020
1359
Date: 9-6-2020
897
Date: 26-1-2020
835
|
Let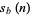 
be the sum of the base-
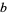digits of 
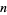, and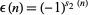 
the Thue-Morse sequence, then
 |
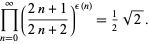REFERENCES:
Allouche, J.-P. "Series and Infinite Products Related to Binary Expansions of Integers." https://algo.inria.fr/seminars/sem92-93/allouche.ps.
Allouche, J.-P. and Cohen, H. "Dirichlet Series and Curious Infinite Products." Bull. London Math. Soc. 17, 531-538, 1985.
Shallit, J. O. "On Infinite Products Associated with Sums of Digits." J. Number Th. 21, 128-134, 1985.
|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|
