


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-8-2020
Date: 9-8-2020
Date: 24-11-2019
|
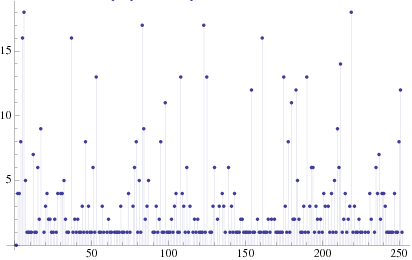
The first few terms of the continued fraction of the Copeland-Erdős constant are [0; 4, 4, 8, 16, 18, 5, 1, ...] (OEIS A030168), illustrated above.
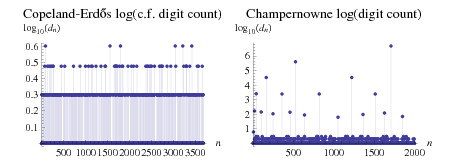
Interestingly, while the Champernowne constant continued fraction contains sporadic very large terms (right figure), making the continued fraction difficult to calculate, the Copeland-Erdős constant has a well-behaved continued fraction that does not show the "large term" phenomenon (left figure).
E. Weisstein computed 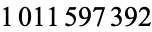 terms of the continued fraction on Jul. 24, 2013.
terms of the continued fraction on Jul. 24, 2013.
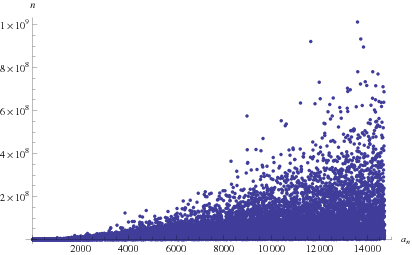
The positions of the first occurrence of 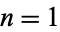 , 2, ... in the continued fraction are 7, 15, 19, 1, 6, 14, 11, 3, 16, 253, ... (OEIS A224891). Smallest numbers not occurring in the first
, 2, ... in the continued fraction are 7, 15, 19, 1, 6, 14, 11, 3, 16, 253, ... (OEIS A224891). Smallest numbers not occurring in the first 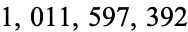 terms of the continued fraction are 14731, 15456, 15579, 15869, ... (E. Weisstein, Jul. 24, 2013).
terms of the continued fraction are 14731, 15456, 15579, 15869, ... (E. Weisstein, Jul. 24, 2013).
The incrementally largest terms are 4, 8, 16, 18, 58, 87, 484, ... (OEIS A033310), which occur at positions 0, 1, 3, 4, 5, 17, 35, 71, 88, 1556, ... (OEIS A224890).
REFERENCES:
Sloane, N. J. A. Sequences A030168, A033310, A224890, and A224891 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|