Least Common Multiple

The least common multiple of two numbers 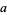 and 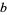, variously denoted  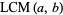(this work; Zwillinger 1996, p. 91; Råde and Westergren 2004, p. 54),  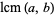(Gellert et al. 1989, p. 25; Graham et al. 1990, p. 103; Bressoud and Wagon 2000, p. 7; D'Angelo and West 2000, p. 135; Yan 2002, p. 31; Bronshtein et al. 2007, pp. 324-325; Wolfram Language), l.c.m. 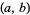(Andrews 1994, p. 22; Guy 2004, pp. 312-313), or , is the smallest positive number 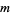 for which there exist positive integers  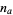and 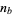 such that

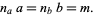(1)

The least common multiple 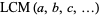 of more than two numbers is similarly defined.

The least common multiple of 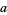, , 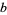... is implemented in the Wolfram Language as LCM[a, b, ...].

The least common multiple of two numbers 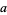 and 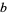 can be obtained by finding the prime factorization of each

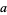			(2)
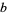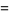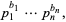			(3)

where the 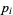s are all prime factors of  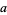and 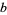, and if  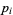does not occur in one factorization, then the corresponding exponent is taken as 0. The least common multiple is then given by

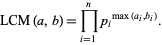(4)

For example, consider .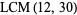

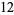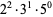			(5)
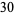			(6)

so

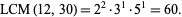(7)

The plot above shows  for rational 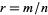, which is equivalent to the numerator of the reduced form of .

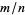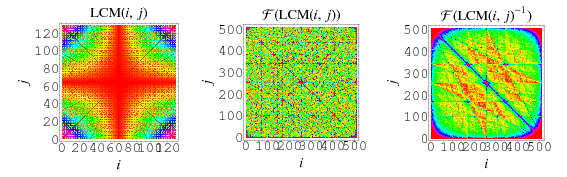
The above plots show a number of visualizations of 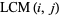 in the 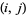-plane. The figure on the left is simply 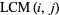, the figure in the middle is the absolute values of the two-dimensional discrete Fourier transform of  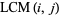(Trott 2004, pp. 25-26), and the figure at right is the absolute value of the transform of .

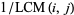The least common multiples of the first 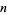 positive integers for 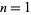, 2, ... are 1, 2, 6, 12, 60, 60, 420, 840, ... (OEIS A003418; Selmer 1976), which is related to the Chebyshev function 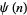. For 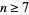,  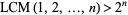(Nair 1982ab, Tenenbaum 1990). The prime number theorem implies that

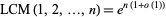(8)

as 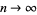, in other words,

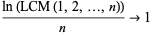(9)

as .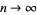

Let 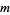 be a common multiple of  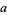and 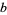 so that

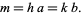(10)

Write 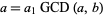 and 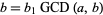, where  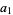and 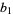 are relatively prime by definition of the greatest common divisor 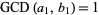. Then 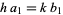, and from the division lemma (given that  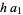is divisible by  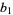and 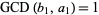), we have  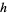is divisible by , so

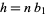(11)

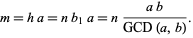(12)

The smallest 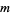 is given by ,

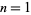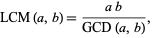(13)

so

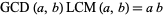(14)

The LCM is idempotent

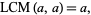(15)

commutative

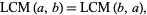(16)

associative

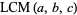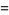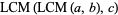			(17)
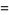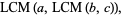			(18)

distributive

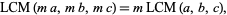(19)

and satisfies the absorption law

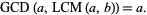(20)

It is also true that

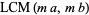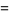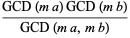			(21)
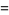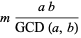			(22)
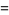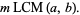			(23)

REFERENCES:

Andrews, G. E. Number Theory. New York: Dover, 1994.

Bressoud, D. M. and Wagon, S. A Course in Computational Number Theory. London: Springer-Verlag, 2000.

Bronshtein, I. N.; Semendyayev, K. A.; Musiol, G.; and Muehlig, H. Handbook of Mathematics, 5th ed. Berlin: Springer, 2007.

D'Angelo, J. P. and West, D. B. Mathematical Thinking: Problem-Solving and Proofs, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000.

Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, 1989.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, 1990.

Guy, R. K. "Density of a Sequence with l.c.m. of Each Pair Less than ." §E2 in Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, pp. 312-313, 2004.

Jones, G. A. and Jones, J. M. "Least Common Multiples." §1.3 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 12-13, 1998.

Nagell, T. "Least Common Multiple and Greatest Common Divisor." §5 in Introduction to Number Theory. New York: Wiley, pp. 16-19, 1951.

Nair, M. "A New Method in Elementary Prime Number Theory." J. London Math. Soc. 25, 385-391, 1982a.

Nair, M. "On Chebyshev-Type Inequalities for Primes." Amer. Math. Monthly 89, 126-129, 1982b.

Råde, L. and Westergren, B. Mathematics Handbook for Science and Engineering. Berlin: Springer, 2004.

Selmer, E. S. "On the Number of Prime Divisors of a Binomial Coefficient." Math. Scand. 39, 271-281, 1976.

Sloane, N. J. A. Sequence A003418/M1590 in "The On-Line Encyclopedia of Integer Sequences."

Tenenbaum, G. Introduction à la théorie analytique et probabiliste des nombres. Publications de l'Institut Cartan, pp. 12-13, 1990.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. https://www.mathematicaguidebooks.org/.

Yan, S. Y. Number Theory for Computing, 2nd ed. Berlin: Springer, 2002.

Zwillinger, D. (Ed.). "Least Common Multiple." §2.3.6 in CRC Standard Mathematical Tables and Formulae, 30th ed. Boca Raton, FL: CRC Press, p. 91, 1996.