
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-8-2019
Date: 29-6-2019
Date: 25-4-2019
|
A delta sequence is a sequence of strongly peaked functions for which
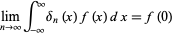 |
(1) |
so that in the limit as 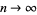 , the sequences become delta functions.
, the sequences become delta functions.
Examples include
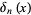 |
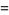 |
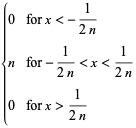 |
(2) |
 |
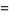 |
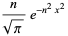 |
(3) |
 |
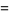 |
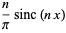 |
(4) |
 |
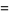 |
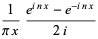 |
(5) |
 |
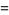 |
![1/(2piix)[e^(ixt)]_(-n)^n](http://mathworld.wolfram.com/images/equations/DeltaSequence/Inline16.gif) |
(6) |
 |
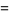 |
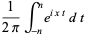 |
(7) |
 |
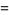 |
![1/(2pi)(sin[(n+1/2)x])/(sin(1/2x))](http://mathworld.wolfram.com/images/equations/DeltaSequence/Inline22.gif) |
(8) |
(Arfken 1985, pp. 482 and 488-489).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.



|
|
|
|
دراسة: النوم غير المنتظم يزيد فرص الإصابة بأمراض
|
|
|
|
|
|
|
العلماء الروس يطورون مسيرة لمراقبة حرائق الغابات
|
|
|
|
|
|
|
انطلاق فعّاليات اليوم الثاني لمؤتمر العميد العلميّ العالميّ السابع
|
|
|