Goursat Problem
المؤلف:
Courant, R. and Hilbert, D
المصدر:
Methods of Mathematical Physics, Vol. 2. New York: Wiley, 1989.
الجزء والصفحة:
...
13-7-2018
2044
Goursat Problem
For the hyperbolic partial differential equation
on a domain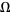 
, Goursat's problem asks to find a solution 
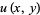of (3) from the boundary conditions
for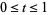 
that is regular in 
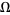and continuous in the closure 
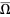, where 
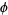and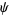 
are specified continuously differentiable functions.
The linear Goursat problem corresponds to the solution of the equation
 |
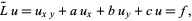(7)
|
which can be effected using the so-called Riemann function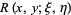 
. The use of the Riemann function to solve the linear Goursat problem is called the Riemann method.
REFERENCES:
Courant, R. and Hilbert, D. Methods of Mathematical Physics, Vol. 2. New York: Wiley, 1989.
Goursat, E. A Course in Mathematical Analysis, Vol. 3: Variation of Solutions and Partial Differential Equations of the Second Order & Integral Equations and Calculus of Variations Paris: Gauthier-Villars, 1923.
Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia." Dordrecht, Netherlands: Reidel, p. 289, 1988.
Tricomi, F. G. Integral Equations. New York: Interscience, 1957.
الاكثر قراءة في المعادلات التفاضلية الجزئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
